The Book
Metaphors Be With You: A Tireless Work On Play On Words
Copyright © 2015 Richard Madsen Neff
Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version 1.3 or any later version published by the Free Software Foundation; with the Invariant Sections being "(", with the Front-Cover Texts being "Metaphors Be With You: A Tireless Work On Play On Words", and no Back-Cover Texts.
A copy of the license is included in the section entitled ‘‘GNU Free Documentation License’’.
-~-~-~-~-~-
- To my Dad
for inspiring me to get 'er done.
-~-~-~-~-~-
1 (
Groucho Marx once quipped, "Outside of a dog, a book is a man's best friend. Inside of a dog, it's too dark to read." This book is not about that kind of word play. (These are not the droids you're looking for. Move on.) But it will have something to say about Outside versus Inside in a logical context later on.
Kith and kin to word play is the idea of transformation, new from old. Old is known, new unknown. The unknown is daunting unless and until it becomes known. And the becoming process is called learning, a transformation from an old state of (less) knowledge to a new state of (more) knowledge.
1.1 Topics To Be Explored
The field of knowledge called discrete mathematics is HUGE — and no wonder; it is like a catch-all net. Anything not contemplated by mathematics of the continuous variety (calculus and company) is considered discrete (but not discreet). So narrowing the scope is a challenge of near epic proportions — met by allowing the following topic pairs to serve as guideposts as we venture out into this vast field.
- Sets and Logic
- Functions and Relations
- Combinatorics and Probability
- Number Theory and Practice
- Trees and Graphs
- Languages and Grammars
Functions (which build on sets (which build on logic)) embody transformations. These are natural, foundational topics in a study of discrete mathematics. And to provide a transformative learning experience, functional programming (the oft-neglected (by most students) odd duck of the programming world) will be a particular focus of this work.
There are two main reasons to gain experience with the functional paradigm. One, functional programming rounds out the dyad of procedural and object-oriented programming, presumably already in the typical programmer's toolbox. Two, learning functional programming is a natural way to learn discrete mathematics, especially since functions are a key aspect, and illuminate many other aspects of discrete mathematics.
For reasons revealed à la Isaiah 28:10, the language of choice for learning functional programming will be the lisp programming language, specifically the Emacs lisp (elisp) dialect. Why lisp, certainly, but especially why elisp? To forestall unbearable suspense, let's dispense with the knee-jerk objection that elisp is not a pure functional programming language. With discipline it can be used as such, and the effort will be instructive.
| Procedural | Object-Oriented | Functional |
|---|---|---|
| Variable values vary. | Same as Procedural. | Variable values never change once assigned. |
| Collections are mutable. | Same as Procedural. | Collections are immutable. |
| Code is stateful (function calls can have side effects). | Same as Procedural. | Code is stateless (function calls can be replaced by their return values without changing program behavior). |
| Functions are partial (not defined on all inputs, so exceptions can be thrown). | Same as Procedural. | Functions are total (defined on all inputs, so exceptions are not thrown, and need not be handled.) |
The above table doesn't capture all the distinctions in this three-way comparison, but one thing is obvious. When looked at through the functional lens, procedural and object-oriented are the same. What then distinguishes them? Mainly what types can be the values of variables. Object-oriented adds user-defined types to the standard primitives and composites of procedural.
P-L and O-O also differ on how they treat nouns and verbs. It gets pretty topsy-turvy when normal everyday distinctions between nouns (things) and verbs (actions) are blurred. When not only do nouns get verbed, but verbs get nouned, we have a double play on words!
Speaking of double, combinatorics, the study of combining, or counting, and number theory, the study of integers (useful for counting — especially the positive ones) are an integral ☺ part of discrete math. How many ways are there of combining things in various combinations? Variations, arrangements, shufflings — these are things that must be accounted for in the kind of careful counting that is foundational for discrete probability theory. But they also come into play in modern practices of number theory like cryptology, the study of secret messages.
Double encore: two more discrete structures, with a cornucopia of applications, are trees and their generalization, graphs. Trees and graphs are two of the most versatile and useful data structures ever invented, and will be explored in that light.
Teaser begin, a binary tree — perhaps the type easiest to understand — can represent any conceptual (as opposed to botanical) tree whatsoever. How to do so takes us into deep representational waters, but we'll proceed carefully. And because graphs can represent relations, listed above in conjunction with functions, they truly are rock solid stars of math and computer science. The relationship between functions and relations is like that of trees and graphs, and when understood leads to starry-eyed wonder, end teaser.
Last double: finishing off and rounding out this relatively small set of topics is the dynamic duo, languages and grammars. Language is being used, rather prosaically, as a vehicle for communication, even as I write these words, and you read them. There is fascinating scientific evidence for the facility of language being innate, inborn, a human instinct. Steven Pinker, who literally wrote the book on this, calls language a "discrete combinatorial system", which is why it makes total sense that it be in this book and beyond.
And what is grammar? Pinker in his book is quick to point out what it is not. Nags such as "Never end a sentence with a preposition," "Don't dangle participles," and (my personal favorite) "To ever split an infinitive — anathema!" Such as these are what you may have learned in "grammar school" as teachers tried their best to drill into you how to use good English. No doubt my English teachers would cringe at reading the last phrase of the last sentence of the last paragraph, where "it" is used in two different ways, and "this book" can ambiguously refer to more than one referent — think about it.
No, in the context of discrete mathematics, grammar has nothing to do with proper English usage. Instead, a grammar (note the indefinite article) is a generator of the discrete combinations of the language system. These generated combinations are called phrase structures (as opposed to word structures), hence, in this sense grammars are more precisely known as phrase structure grammars. But we're getting ahead of ourselves — PSG ISA TLA TBE l8r.
1.2 Autobiographical Aside
I am writing this book for many reasons, which mostly relate to the following language-ish math-ish relationships and transformations: Words have Letters, Numbers have Digits, Letters map to Digits, hence Words map to Numbers.
I love words. I love numbers. Does that mean English was my first choice of discipline, Math second? No! English is my native tongue, but Math to me feels PRE native, or the language I came into this world furnished with. Not that I lay claim to being a mathematical prodigy like Fredrich Gauss, John Von Neumann, or any extraordinary human like that. Not even close!
A first recollection of my inchoate interest in math is from third grade. There I was, standing at the blackboard, trying to figure out multiplication. The process was mysterious to me, even with my teacher right there patiently explaining it. But her patience paid off, and when I "got it" the thrill was electrifying! Armed with a memorized times table, I could wield the power of this newly acquired understanding. Much later in life came the realization that I could immensely enjoy helping others acquire understanding and thus wield power!
Back to words. As I said, I love them. I love the way words work. I love the way they look. I love the way they sound. Part of this stems from my love of music, especially vocal music. Singers pay attention to nuances of pronunciation, 5 being but one example. Take another example. The rule for pronouncing the e in the. Is it ee or uh? It depends not on the look of the next word but its sound. The honorable wants ee not uh because the aitch is silent. The Eternal, but the One — ee, uh. Because one is actually won.
The attentive reader may have noticed that, among other infelicities, the preceding paragraph plays fast and loose with use versus mention. There is a distinction to be made between the use of a word, and the mention of a word.
For example, the word Idaho:
Idaho has mountains. (A use of the word.)
'Idaho' has five letters. (A mention of the word.)
This distinction will come to the fore when expressions in a programming language like lisp must be precisely formed and evaluated. The quote marks are all-important. Small marks, big effect.
Analogously, what importance does a simple preposition have? How about the crucial difference between being saved in your sins versus being saved from your sins! Small words, enormous effect.
I have a well-nigh fanatical fondness for the English alphabet with its 26 letters. 26 is 2 times 13. 2 and 13 are both prime, which is cool enough, but they're also my birth month and day. And it's unambiguous which is which. 2/13 or 13/2 — take your pick. Because there's no thirteenth month, either way works. Not every birth date is so lucky! Not every language's alphabet is so easy, either.
Despite the coolness of twice a baker's dozen, it is deficient by one of being an even cooler multiple of three, and that's a state of affairs we'll not long tolerate. But which non-alphabetic (and non-numeric) symbol is best pressed into service to bring the number to three cubed?
Twenty-seven is three times nine. Nine give or take three is the number of main topics. Three chapters (not counting opening and closing bookends), with each chapter having at least three sections, each section having at least three subsections — perhaps bottoming out at this level — this seems to me to be a pretty good organization.
Slice it. Dice it. No matter how you whatever ice it — notice it's not ice (but is it water — whatever hve u dehydrated?!) — 'alphabet' is one letter shy of being a concatenation (smooshing together) of the first two letters of some other (which?) alphabet. So correct its shyness (and yours). Say alphabeta. Go ahead, say it! Now say ALP HAB ETA (each is pronounceable) — but don't expect anyone to understand what you just said!
1.3 TOP is the TLA
The Organizing Principle I have chosen for this book is the Three-Letter Acronym.
Why? Well, it fully fascinates me that "TLA ISA" is a perfectly grammatical sentence if interpreted just so. It expresses concisely the truth: 'TLA' "self-describes" (which is another intriguing saying).
But TLA can also stand for Three-Letter Abbreviation, of which
there are many, (JAN FEB MAR APR MAY JUN JUL AUG SEP OCT NOV DEC)
being but one example.
Replacing the 'A' in TLA with a 'W' gives TLW, an acronym for
Three-Letter Word — (TOP TOE TON TOT TOY) for a butcher's
half-dozen of which.
Note that we could generate this list by simply prefixing TO to
each letter in PENTY, a carefully chosen way to code-say Christmas.
Note too that neither this list of five TLWs nor the first list of twelve TLAs has commas, those typical list item separators. The comma-free rendering is deliberate and significant, as will be seen.
Back to playing with words. If you can eat your words, shouldn't you be able to smell and taste them too?! Or play with words like you play with your food? (These are rhetorical questions — don't try to answer them!)
Scrambled EGGS — (GSGE GESG SGEG ...)
Can all 12 (not 24! (which is NOT to say 24 factorial (which equals 620448401733239439360000, IYI))) arrangements be put into one tetragramamalgam? What's a tetragramamalgam? (These are NOT rhetorical questions — DO try to answer them!)
So there you have it. An assorted set of words and "words" to guide discovery. Many to unpack meaning from. If the metaphor is a good one, that meaning gets packed into words, (or encodings thereof (another layer of packing material)), then unpacking can result in rich interconnected structures that strengthen learning, that make it stick in the brain. And that that permanently (it is hoped) stuck learning will serve you well is my high hope.
2 ONE
He awoke with a start. What time was it? … Did his alarm not go off? … No, it was 3:45, he just woke up too early. He lay there, mind racing, trying to figure out what had woken him up. His wife was breathing deeply, she was sound asleep, so it wasn't her stirring. No … it was that dream. That awesome, awefull dream where he was outside staring into the clear night sky, basking in "the icy air of night" when suddenly he felt a very real vertigo, as if he were falling up into that endless star-sprinkled void.
Falling up. A contradiction in terms. Yes, but one to be embraced, not shunned, because it gives one an EDGE. No, this is the title of a book. Yes, that treasured book he had acquired years ago, and still enjoyed. Clever poems and cute drawings. It was because the author was so playful with words and the thoughts they triggered that he liked it, and his other book, what was it? Where The Sidewalk Ends. Yes, well, enough of that. He would have to get up soon. Today he would meet his two new tutees. TWOtees for short. A male and a female had seen his ad and responded. Was he expecting more than two to? Yes … but two would be fine. Two would be enough to keep him busy.
-~-~-~-~-~-
"What I'd like to do today is just make introductions and see where we're at," he said. "My name is Tiberius Ishmael Luxor, but you can call me Til. T-I-L, my initials, my preference." While escorting his two visitors into his study, his mind wandered, as it always did when he introduced himself. Tiberius, why had his parents, fervent fans of Captain Kirk and all things Star Trek, named him that? And Ishmael? Was Moby Dick also a source of inspiration? Or the Bible? He had never asked them, to his regret. Luxor, of course, was not a name they had chosen. He rather liked his family name. The first three letters, anyway. Latin for light. He often played with Luxor by asking himself, Light or what? Darkness? Heavy? Going with the other meaning of light seemed frivolous.
"Uh, my name's Atticus. Atticus Bernhold Ushnol," his male visitor said, noticing that Til looked distracted. "What do you prefer we call you?" asked Til, jerking himself back to full attention. "Well, I like Abu, if that's okay with you!"
Til smiled. A man after his own heart. "How acronymenamored of you!" he said.
"Is that even a word?" asked his female guest, addressing Til. Feeling just a little annoyed, she turned to Abu and said "You really want us to call you the name of the monkey in Aladdin?" Abu smiled, a crooked grin. "Well, I wouldn't know about that — I never saw Aladdin."
"How could you not have seen Aladdin? What planet are you from?" she said, completely incredulous.
"Hold on a minute," said Til. "Let's discuss the finer points of names and origins after you introduce yourself."
"Ila. My middle name is my maiden name, Bowen. My last name is my married name, Toopik, which I suppose I'm stuck with." Ila always felt irritated that marriage traditionally involved changing the woman's name, not the man's. "And yes, it's Eee-la, not Eye-la. And I especially prefer you don't call me Ibt, if you get my drift!"
Til laughed. Abu was still grinning but said nothing, so Til went on. "We need variety, so Ila is fine. Not everyone needs to be acronymized!"
-~-~-~-~-~-
Later that day as Til reflected on their first meeting, he saw himself really enjoying the teacher-learner interactions to come. His ad had had the intended effect. Abu and Ila were motivated learners, albeit for different reasons. He was somewhat surprised that not more interest had been generated. But he knew it was unlikely up front. So two it would be. Two is a good number. Three is even better (odd better?) if he counted himself as a learner. Which he always did. Learning and teaching were intricately intertwined in his mind. Teaching was like breathing, and both teaching and learning were exhilarating to Til.
His wife interrupted his reverie. "Til, dear, what did you learn today from your first meeting with — what did you call them — Abu and Ila?"
"Interesting things," said Til. "Abu is the general manager at a landscaping company (I think he said nursery as well). Ila works for some web design company (I forget the name) doing programming. She wants to learn discrete math because she's been told it will make her a better programmer!"
"However, Abu's not a programmer, and not really all that techy, I gathered, but says he loves learning, practical or not. I predict this may put him at odds at times with Ila, who said she only wants practical learning. I told her Euclid would mock that attitude, and she was surprised. But she agreed to look into that. She didn't know who Euclid was, if you can imagine!" Til winked his eye, and his wife rolled hers.
"Anyway, Abu's pretty laid back, so her barbs won't bother him — much I hope," he said.
"Are they married, any kids?" she said.
"Abu is single, but would like to be married." Til rubbed his chin. "Ila is married, but she didn't mention her husband's name, or really anything about him, except that he's not a nerd like her. Before they even warmed up to my affinity for acronyms, Ila confessed to being a DINK, and Abu immediately responded, 'I guess that makes me a SINKNEM!' So he's pretty quick on the uptake."
"That's good!" she said. "So Ila's husband is not nerdy like her, but …?"
"But she also didn't say what he does," he said. "She taught herself programming, how cool is that?!"
"Very cool, Mr. Luxor," she said affectionately, gently rubbing his shoulders.
"Mrs. Luxor, I'll give you 20 minutes to stop that!" he said.
"What are their interests other than discrete math?" she said, ignoring his pathetic ploy.
"Well, let's see, Abu rattled off his other interests as flowers, stars and poetry!" he said. "And Ila likes sports and the outdoors. Hopefully that includes stars!"
"That would be great if you all have stars in common," she said.
Til nodded, but his eyes unfocused as his thoughts started to wander. His wife withdrew, wordlessly worrying that Til was thinking about sharing his dream about falling up into the stars with Abu and Ila. That never seemed to go well. But Til was remembering the exchange he had with Abu, who lingered a few minutes after Ila left.
He had said, "Abu, since you like flowers, you must be okay with the STEMless reputation they have!" Without waiting for him to answer he went on, "Since I gave Ila an invitation to learn something about Euclid, I invite you to look up what Richard Feynman said about flowers and science, specifically whether knowing the science made him appreciate the flowers more or less?"
Well, enough musing for now. His two tutees were eager and grateful, and not just because they thought the fee he had set was reasonable. Little did they know the price of knowledge he would exact of them.
-~-~-~-~-~-

2.1 ABC
When you read you begin with A, B, C; when you sing you begin with Do, Re, Mi; when you count you begin with 1, 2, 3 — or is it 0, 1, 2?! Mathematicians do both, and have logical reasons for each. Computer scientists mainly do zero-based counting, as coaxed to do by both hardware and software. 0-1-2; ready-set-goo!
So let's begin with the set of positive integers, also known as the counting numbers — except, wait. How do you count the number of elements in the set with no elements, AKA the empty set? You need zero, which for centuries was not even considered a number. Lucky for us, these days zero is a full-fledged member of the set of natural numbers, another name for the counting numbers. But some still see zero as UNnatural and thus exclude it from the set. Right away, ambiguity rears its hoary head, and definitions must needs be clarified before crafting arguments that depend on whether zero is in or out.
VTO: a set is just a collection of objects, where objects are individual, discrete, separate things that can be named or identified somehow. A collection that serves the mathematical idea of a set is an unordered one — the elements can be listed in any order and it doesn't change the set.
Speaking of lists, LISP originally stood for LISt Processor (or Processing), so let's list some simple sets in lisp style, and show a side-by-side comparison with math style:
| Lisp Style | Math Style |
|---|---|
| () or nil | {} or ∅ |
| (A B C) | {A, B, C} |
| (Do Re Mi) | {Do, Re, Mi} |
| (1 2 3) | {1, 2, 3} |
| (0 1 2) | {0, 1, 2, …} |
Other than dispensing with commas and replacing curly braces with parentheses, lisp is just like math — except, wait. What are those three dots saying? In math, the ellipsis (…) is short for "and so on" which means "continue this way forever". Since lisp is a computer programming language, where doing things forever is a bad idea, we truncated the set N after listing its first three members.
Also, no duplicates are allowed in sets. This requirement guarantees element uniqueness, a desirable attribute strangely yoked with element unorderliness, the other main (anti-)constraint. Here are three lispy sets (really lists):
(A B C) (A A B C) (A A A B C C)
Here are three more:
(B A C) (C A B) (B C A)
But by definition these are all the same set — (A B C) — so
let's just make it a rule to quash duplicates when listing
sets. And since order is implied by the normal left-to-right
listing order, we have a contradictory situation where order is
implied yet irrelevant. That really implies (linked) lists are not
the ideal data structure for representing sets, and (linkless)
vectors in elisp are no better — they are simply indexable arrays
of (heterogeneous or homogeneous) elements — but let's say
our rule also prefers vectors to lists. So the rule
transforms a mathy set like {A, C, C, C, B} into a lisp list (A C
B) and thence to the vector [A C B], which is now in a form that
can be evaluated by the lisp interpreter built into emacs (a later
lesson shows how lists can be evaluated too):
VTO: an expression expresses some value in some syntactic form, and to evaluate means to reduce an expression to its value (for the purpose of handing it off to some further processing step).
2.1.1 GIK
We next turn our attention to a way to view statements about sets as propositions with Boolean values (true or false). In lisp, true is abbreviated t, and false nil. With some help from a pair of global variables, we can be traditional and just use true and false.
VTO: a proposition is a sentence (or statement) that is either true or false. The sentence can be about anything at all (not just sets), as long as ascertaining its truth or falsity is feasible. The study called propositional logic deals with standalone and compound propositions, which are propositions composed of other propositions, standalone or themselves composite. How to compose or combine propositions to create these compounds is coming after a few exercises in model building. Do start the warmup by thinking up three examples and three non-examples of propositions. Make them pithy.
True propositions are AKA facts. A set of true propositions is called a knowledge base, which is just a database of facts. This set represents what we know about the world (or a subset of the world) or, in other words, the meaning or interpretation we attach to symbols (such as sentences — strings of words). Take a simple two-proposition world:
- It is true that snow is white.
- It is false that grass is white.
Given our propensity for abbreviation, let's assign propositional
variables p and q to make it easier to manipulate this world:
p= "snow is white"q= "grass is white"
p and not q represents our interpretation of this world. We could
imagine a stranger world — stranger than the real one where we
live — where p and q (i.e., where snow is white and so is
grass) or even not p and q (where snow is green, say, and grass
is white) is the real model.
VTO: a model is (roughly speaking) the meanings (interpretations) of symbols. In general, a model is all over the map, but in propositional logic, models are assignments of truth values to propositions (conveniently identified as variables). As aforementioned, truth values are Boolean values, true or false. Period. No partly true or somewhat false, nor any other kind of wishy-washiness.
Decision-making ability is an important component of any
programming language. Lisp is no exception. The conditional logic
decidering of one of the basic logical connectives will be
revealed in the following exercise that invites you to explore the
logical connectives and (∧), or (∨), xor (⊕), and
not (¬). Naturally, not is not a connective in the sense of
connecting two things together, but it's a logical operator
nonetheless. For xor, the 'exclusive' or, use the if form to do
a conditional expression.
2.1.2 MOQ
We can compose or combine propositions to create compound propositions by applying the following rules again and again (consider this a 'grammar' for generating these propositional 'molecules' from propositional 'atoms'):
- A
propositionis a variable, that is, a single element from the set[p q r s t ...]; - alternatively, a
propositionis apropositionpreceded by anot; - alternatively, a
propositionis apropositionfollowed by aconnectivefollowed by aproposition. - A
connectiveis a single element from the set[and or xor].
Rules 2 and 3 have a recursive flavor, so said because they refer back to themselves; that is, they define a proposition in terms of itself, and simpler versions of itself.
We actually need more syntactic structure to make sense of certain compounds. For example, building a proposition from scratch by starting with
proposition;
from thence applying rule 1 (choosing p) then rule 3 yields
p connective proposition;
from thence applying rule 4 (choosing and) yields;
p and proposition;
from thence applying rule 3 again yields
p and proposition connective proposition;
from thence applying 1 twice and 2 once yields
p and q connective not r;
from thence one more application of 4 (choosing or) yields the
not-further-expandable:
p and q or not r
Which is ambiguous. Does it mean p and s where s is q or
not r? Or does it mean s or not r where s is p and q? In
other words, which is the right interpretation, 1 or 2?
p and (q or not r); associating from the right.(p and q) or not r; associating from the left.
The mathematically astute reader will recognize that the parentheses are the extra syntactic sugar we need to sprinkle on to disambiguate (choose 1 or 2 (but not both)).
The next question is, does it matter? Try it both ways with the
truth-value assignment of p to true, q to false, and r
to true:
Replacing p, q, and r with true, false, and true,
respectively, in
p and (q or not r)
yields
true and (false or not true)
Before simplifying this expression, a quick review of how these connectives work:
The simplest one first: not flips truth values — when notted
(or negated — not is AKA negation) true becomes false, false
becomes true. To be true, or requires at least one of the two
propositions appearing on its left-hand-side (LHS) and its
right-hand-side (RHS) to be true. If both of them are false, their
disjunction (a fancier name for or) is false. To be true, and
requires both propositions (LHS and RHS) to be true. If even one
of them is false, their conjunction (a fancier name for and) is
false.
Back to the task: the above expression simplifies to
true and (false or false)
from thence to
true and false
from thence to
false.
Replacing propositional variables with their values in
(p and q) or not r
yields
(true and false) or not true
which simplifies to
(true and false) or false
from thence to
false or false
and finally
false.
So they're the same. But wait! What if we try a different
assignment of truth values? With all of p, q and r false, here is
the evolving evaluation for 1 (p and (q or not r)):
false and (false or not false)false and (false or true)false and truefalse
And here it is for 2 ((p and q) or not r):
(false and false) or not falsefalse or not falsefalse or truetrue
So it's different — it DOES matter which form we choose. Let's tabulate all possible truth-value assignments (AKA models) for each, and see how often they're the same or not:
First, how do we generate all possible assignments? Let's use a decision tree:
p q r
/ false false false
/\ false false true
/\/ false true false
/ \ false true true
\ / true false false
\/\ true false true
\/ true true false
\ true true true
In this binary tree, each node (wherever it branches up or down) represents a decision to be made. Branching up represents a choice of false, branching down true. Going three levels (branch, twig, leaf) gives us the eight possibilities.
VTO: a tabulation of possible models (essentially picking off the leaves of the tree from top to bottom (making each leaf a row)) is called a truth table. Here's an example:
| p | q | r | not r | (q or not r) | (p and (q or not r)) |
|---|---|---|---|---|---|
| false | false | false | true | true | false |
| false | false | true | false | false | false |
| false | true | false | true | true | false |
| false | true | true | false | true | false |
| true | false | false | true | true | true |
| true | false | true | false | false | false |
| true | true | false | true | true | true |
| true | true | true | false | true | true |
Numerically it makes sense to have, and indeed most other languages
do have, 0 represent false. Lisp is an exception — 0 evaluates
to non-nil (which is not nil — not false). Having 1 represent
true has advantages, too, although MOL treat anything non-zero as
true as well. Still, it's less typing, so we'll use it to save
space — but keep in mind, the arithmetization of logic is also
instructive because of how it enables certain useful encodings.
Here's the same truth table in a more compact form:
| (p | ∧ | (q | ∨ | ¬ | r)) |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 1 | 0 |
| 0 | 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 | 1 | 0 |
| 0 | 0 | 1 | 1 | 0 | 1 |
| 1 | 1 | 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 | 0 |
| 1 | 1 | 1 | 1 | 0 | 1 |
2.1.3 SUW
Let it be. Let it go. Let it go so. Let it be so. Make it so.
Let p be prime. In lisp, something like p is called a symbol,
and you can treat a symbol essentially like a variable, although
it is much more than that.
Let something be something is a very mathy way of speaking. So lisp
allows somethings to be other somethings by way of the keyword
let.
Like God, who said let there be light, and there was light, the
programmer commands and is obeyed. The keyword let binds symbols
to values, fairly commanding them to stand in for values. Values
evaluate to themselves. Symbols evaluate to the values they are
bound to. An unbound symbol cannot be evaluated. If you try it, an
error results.
Before doing some exercises, let's look at let syntactically and
abstractly:
(let <frame> <body>)
The <frame> piece is a model in the form of a list of bindings.
Just as we modeled truth-value assignments as, e.g., p is true
and q is false, in list-of-bindings form this would be ((p
true) (q false)). A binding is a two-element list (<var>
<val>). Variables can be left unbound, so for example, (let
((a 1) (b 2) c) ...) is perfectly acceptable. It assumes c will
get a value later, in the <body>.
The <body> is a list of forms to be evaluated — forms that use
the bindings established in the frame model.
The frame list can be empty, as in:
(let () 1 2 3) ; alternatively (let nil 1 2 3)
The value of this symbolic expression (lispers shorten this to an s-expression, or sexp for shorter) is 3, the value of the last form before the closing parenthesis.
2.1.4 YAC
The rule for dealing with lisp expressions is to look for lists,
and when found, evaluate them. Casual observation reveals the bulk
of lisp code is in fact lists, and lists of lists nested to many
levels. Evaluating a list entails evaluating each of its elements,
except the first, which is treated differently. For now, think of
the first element as an operator that operates on the values of
the rest of the elements. So (+ 1 2 3 4) adds together 1 (the
value of 1 — numbers self-evaluate), 2, 3 and 4 to
produce 10. Note the economy of this prefix notation, as it's
called: only one mention of the '+' sign is needed. The more
familiar infix notation requires redundant '+' signs, as in
1+2+3+4.
2.1.5 EGI
CSP a description of set operations, union, intersection, difference, symmetric difference, subset-of, superset-of, disjoint, mutually or not; De Morgan's laws for logic and sets.
| p | q | p ∧ q | p ∨ q | p ⊕ q |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 1 | 1 |
| 1 | 1 | 1 | 1 | 0 |
2.2 DEF
Til has assigned a LOT of homework. Ila complains to Abu about it. Abu is sympathetic.
"I mostly get the logical connectives, which why we don't just call them operators is what I don't get. They're the same as the logical operators in JavaScript, and …" Abu interrupted Ila's rant. "What's JavaScript?", he asked. "It's a programming language — the one I mostly program in. Anyway, what I also don't get is the conditional operator. It just seems illogical that it's defined the way it is. How did Til put it?"
"I believe he said 'p only if q is true, except when p is more true than q'," said Abu.
"That's what I'm talking about, what does 'more true than' mean? Something is either true or it's not. How can it be 'more true'? Truer than true??"
"Well, here's how I see it," said Abu. "When they have the same truth value, both true or both false, neither is more or less than the other, they're equal."
Ila felt her face go red. "Oh, now I get it — a true p is greater than a false q. And the last case, when p is false and q is true, p is less true than q. Way less, because it has zero truth."
"Irrelevant to the truth of q," said Abu. "I drew its truth table, like Til asked, and only one row is false, the rest true. Perhaps you drew it this way too?"
| p | q | p → q |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Ila frowned. "Mine has the last column centered under the arrow, but otherwise it's the same as yours."
"I like centered better," said Abu. "Til will be glad we get it, I think, but do you think he was going to explain it some more?"
"He will if we ask, but I don't want to ask him — will you?" said Ila. "No problem," said Abu. "I don't mind appearing ignorant, because appearances aren't deceiving in my case — I really AM ignorant!" "Well, I hate asking dumb questions," said Ila. "Never been a problem for me," said Abu with a slow exhalation.
Ila voiced her other main complaint. "And I'm still floored that he said, go learn lisp, it will do you good." Abu nodded. "I agree that seems like a lot to ask, but I'm enjoying the challenge. Lisp is cool!" Ila sighed. "It certainly lives up to its name: Lots of Irritatingly Silly Parentheses, and if you ask me, it's just confusing." Abu smiled. "I found this xkcd comic that compares lisp to a Jedi's lightsaber. See, I got the Star Wars reference. And by the way, just to show you what planet I'm from, I went and watched Aladdin. So let's see, Chewbacca is Abu to Han Solo's Aladdin, right!" "Hardly," said Ila. "So you saw the movie and you still want us to call you Abu?!"
-~-~-~-~-~-
"Think of it this way," said Til. "Inside versus Outside. With your pads draw a couple of circles, two different sizes, the smaller inside the larger. Make them concentric. Okay? Now consider the possibilities. Can something be inside both circles simultaneously?"
Abu and Ila nodded simultaneously.
"That's your p-and-q-both-true case. Now, can something be outside both circles? Yes, obviously. That's your p-and-q-both-false case. And can something be inside the outer circle without being inside the inner one? Yes, and that's when p is false and q is true."
Ila was feeling a tingle go up her spine. She blurted, "I see it! The only impossibility is having something inside the inner circle but not inside the outer — p true and q false. Makes perfect sense!"
Til beamed. "You got it, Ila! How about you, Abu?"
Abu just smiled and nodded his head.
"Would you please explain 'let' more?" said Ila. She was getting past her reluctance to ask questions, and it felt great!
"Think cars," said Til. "A car has a body built on a frame, just like a let has a body built on a frame. But without an engine and a driver, a car just sits there taking up space. The lisp interpreter is like the engine, and you, the programmer, are the driver."
Abu had a thought. "A computer also has an engine and a driver, like processor and programmer, again. But cars contain computers, so I doubt equating a car with a computer makes sense."
Til agreed. "You see a similarity but also a big difference in the two. A car is driven, but the only thing that results is moving physical objects (including people) from here to there. That's all it does, that's what it's designed to do. But a computer is designed to do whatever the programmer can tell it to do, subject to the constraints of its design, which still — the space of possibilities is huge."
Ila was puzzled. "Excuse me, but what does this have to do with 'let'?"
Til coughed. "Well, you're right, we seem to be letting the analogy run wild. Running around inside a computer are electrons, doing the "work" of computation, electromagnetic forces controlling things just so. It's still electromagnetics with a car, for example, combustion of fuel. But these electromagnetic forces are combined with mechanical forces to make the car go."
"Just think of 'let' as initiating a computational process, with forces defined by the lisp language and interacting via the lisp REPL with the outside world. Then letting computers be like cars makes more sense. Do you recall that a lisp program is just a list?"
Abu nodded, but interjected. "It's really a list missing its outermost parentheses, right?"
Til's glint was piercing. "Ah, but there's an implied pair of outermost parentheses!"
Ila fairly stumbled over her tongue trying to blurt out. "And a 'let nil' form!"
Now it was Abu's turn to be puzzled. He said, "Wait, why nil?" Ila rushed on, "It just means that your program can be self-contained, with nil extra environment necessary to run. Just let it go, let it run!"
2.2.1 KMO
Let's leave 'let' for now, and look at lisp functions via the defun special form.
(defun <parameter-list> [optional documentation string] <body>)
Examples of /def/ining /fun/ctions via defun are
forthcoming. First note that this language feature is convenient,
but not strictly necessary, because any function definition and
call can be replaced with a let form, where the frame bindings
are from the caller's environment.
For example, the function list-some-computations-on, defined and
invoked (another way to say called) like this:
(defun list-some-computations-on (a b c d) "We've seen this one before." (list (+ a b) (/ d b) (- d a) (* c d))) (list-some-computations-on 1 2 3 4)
This definition/call has exactly the same effect as:
(let ((a 1) (b 2) (c 3) (d 4)) (list (+ a b) (/ d b) (- d a) (* c d)))
Of course, any procedural (or object-oriented) programmer knows why the first way is preferable. Imagine the redundant code that would result from this sequence of calls if expanded as above:
(list-some-computations-on 1 2 3 4) (list-some-computations-on 5 6 7 8) ; ... (list-some-computations-on 97 98 99 100)
Functions encapsulate code modules (pieces). Encapsulation enables modularization. The modules we define as functions become part of our vocabulary, and a new module is like a new word we can use instead of saying what is meant by that word (i.e., its definition) all the time.
But stripped down to its core, a function is just an object that takes objects and gives other objects. Speaking completely generally, these are objects in the 'thing' sense of the word, not instances of classes as might be assumed if object-oriented programming were the context. Are there any restrictions on what objects can be the inputs to a function (what it takes) and what objects can be the outputs of a function (what it gives)? Think about and answer this question before looking at the endnote.
VTO: again, a function is simply an object, a machine if you will, that produces outputs for inputs. But simply amazingly, there is a plethora of terms describing various kinds and attributes of functions that have been designed and pressed into mathematical and computer scientific service over the years:
- domain is the term for the set of all possible inputs for a function. (So functions depend on sets for their complete and rigorous definitions.)
- codomain is the set of all possible outputs for a function.
- range is the set of all actual outputs for a function (may be different — smaller — than the codomain).
- onto describes a function whose range is the same as its codomain (that is, an onto function produces (for the right inputs) all possible outputs).
- surjective is a synonym for onto.
- surjection is a noun naming a surjective function.
- one-to-one describes a function each of whose outputs is generated by only one input.
- injective is a synonym for one-to-one.
- injection is a noun naming an injective function.
- bijective describes a function that is both one-to-one and onto.
- bijection is a noun naming a bijective function.
- recursive describes a function that calls itself. Yes, you read that right.
- arguments are the inputs to a function (argument "vector" (argv)).
- arity is short for the number of input arguments a function has (argument "count" (argc)).
- k-ary function — a function with k inputs.
- unary – binary – ternary — functions with 1, 2 or 3 arguments, respectively.
- infix notation describes a binary function that is marked as a symbol between its two arguments (rather than before).
- prefix notation describes a k-ary function that is marked as a symbol (such as a word (like list)) before its arguments, frequently having parentheses surrounding the arguments, but sometimes (like in lisp) having parentheses surrounding symbol AND arguments.
- postfix notation describes a function that is marked as a symbol after its arguments. Way less common.
- image describes the output of a function applied to some input (called the pre-image of the output). (The image of 2 under the 'square' function is 4. The square function's pre-image of 4 is 2.)
Since the square function (a unary, or arity 1 function) is a handy one to have around, we defun it next:
(defun square (number) "Squaring is multiplying a number by itself, AKA raising the number to the power of 2." (* number number))
There are many one-liners just itching to be defuned (documentation string (doc-string for short) deliberately omitted):
(defun times-2 (n) (* 2 n)) (defun times-3 (n) (* 3 n))
This one deserves a doc-string, if only to remind us what the 'x' abbreviates:
(defun xor (p q) "Exclusive or." (if p (not q) q)) (defun not-with-0-1 (p) (- 1 p))
As written, all of these one-liner functions are problematic;
take, for example, not-with-0-1. Its domain is exactly the set
[0 1], and exactly that set is its codomain (and range) too. Or
that's what they should be. Restricting callers of this function
to only pass 0 or 1 is a non-trivial task, but the
function itself can help by testing its argument and balking if
given something besides 0 or 1. Balking can mean many things
— throwing an exception being the most extreme.
2.2.2 QSU
We've been viewing a function a certain way, mostly with a programming bias, but keep in mind that functions can be viewed in many other ways as well. The fact that functions have multiple representations is a consequence of how useful each representation has proven to be in its own sphere and element. A function is representable by each of the following:
- assignment
- association
- mapping (or map)
- machine
- process
- rule
- formula
- table
- graph
and, of course,
- code
CSP examples and exercises.
The bottom line: mathematical functions are useful abstractions of the process of transformation. Computer scientific functions follow suit.
2.2.3 WYA
Let's now define a sequence and distinguish it from a set. The difference is that a sequence is an ordered collection. So a list or a vector is just a sequence, and truth be told, a sequence is really just a special kind of function.
VTO: a finite sequence of elements of a set S is a function
from the set {1, 2, 3, ..., n} to S — the number n is the
length of the string. Alternatively, the domain of the sequence
function can be {0, 1, 2, ..., n - 1} (or with n concretized as
10, [0 1 2 3 4 5 6 7 8 9] in lisp vector style). The sequence
length is still n (ten) in this case.
Generically, an denotes the image of the (nonnegative) integer n, AKA the nth term of the sequence. An infinite sequence of elements of S is a function from {1, 2, 3, …} to S. Shorthand notation for the entire sequence is {an}. Again, the domain can be either Z+ or N.
For example, {an}, where each term an is just three times n
(i.e., a(n) = 3n, or in lisp, (defun a (n) (times-3 n))), is a
sequence whose list of terms (generically a1, a2, a3, a4,
…) would be 3, 6, 9, 12, … (all the multiples of three —
infinite in number).
Another term for a finite sequence is a string, that venerable and versatile data structure available in almost all programming languages. Strings are always finite — if it's an infinite sequence, it is most emphatically not a string.
With lisp symbols there must automatically be support for strings.
Every symbol has a unique string naming it, and everywhere the same
symbol is used, the same string name (retrieved via the function
symbol-name) comes attached.
2.2.4 CEG
Functions that return false (nil) or true (t — actually
anything that evaluates to non nil) are ubiquitous. So much so
that they have a special name — predicate.
VTO: a predicate is a function whose codomain is the set [true
false], and is AKA a property. The domain of a predicate can be
any conceivable set. We could also call these functions deciders
(short for decision-makers) that ascertain whether or not a given
object has a specified property.
2.2.5 IKM
"Applying the plus function to sequences yields summations." Let's
unpack that sentence. To apply a function to a sequence we need
that function's symbol, the sequence as a list, and the function
apply. Here's where we start to see the power of the functional
programming paradigm.
CSP applying '+ (yes, no closing quote is correct) to sequences to get summations.
2.2.6 OQS
Continuing to mind our p's and q's, it's time to talk
predicates and quantifiers.
In our neverending quest for succinctness, we desire a shorter way
to say, for example, all the colors of the rainbow are
beautiful. Shorter, that is, than just listing all true
propositions, with B for Beautiful as predicate:
B(red)B(orange)B(yellow)B(green)B(blue)B(indigo)B(violet)
We know all the colors in the domain, so why not just say, for all the colors in the rainbow, each is beautiful. Or even more succinctly, every rainbow color is beautiful. These quantifiers "all" and "every" apply to the whole of our universe of discourse.
VTO: a universe of discourse (AKA domain of discourse) is the set of all things we've set forth to talk about, i.e., all things under consideration. It must be specified (unless the real universe is the universe of discourse) to make sense of propositions involving predicates. The universal quantifier ∀ says something is true for all members of this universal set, no exceptions.
Saying something like
- ∀
x B(x)
rather than
B(red)∧B(orange)∧B(yellow)∧B(green)∧B(blue)∧B(indigo)∧B(violet)
(because, of course, each and every one is true) is much shorter, which is especially important when the domain is large (or infinite).
- ∀
x Even(x)
is true when x comes from [2 4 6 8 10 12 14 16 18 20 22 24 26
28 30 32 34 36 38 40 42], but false when the domain is [2 4 6 8
10 12 14 16 18 20 22 24 26 28 30 32 34 36 38 40 41], instead. And
indeed
- ∀
x Even(x)
is infinitely shorter than a conjunction of unquantified
propositions Even(2) ∧ Even(4) ∧ …, one for each
member of the set of even integers.
2.2.7 UWY
Another easy example:
Let P = "is a ball".
So P(x) means x is a ball. Is P(x) true?
We can't say. A predicate (or more precisely, a propositional function (or formula) consisting of a predicate and some variable(s)) is not a proposition.
∃ x P(x)
Meaning: There exists an x such that x is a ball.
∃ is the Existential quantifier.
Is this true?
It depends.
What is the Universe of Discourse?
Let it be the set [markers erasers whiteboards] (in a classroom, for example).
¬ ∃ x P(x) means "There does not exist an x such that x is a ball".
(True, in this Universe.)
∃ x ¬ P(x) means "There exists an x such that x is not a ball".
This is the same as saying "Something is not a ball."
But it's not the same as saying "Everything is not a ball."
∀ x ¬ P(x)
Meaning: For every x, it is not the case that x is a ball.
Remember, ∀ is the Universal quantifier.
¬ ∀ x P(x) means "Not everything is a ball".
Let R(y) = "y is red".
∀ y R(y) means "Everything is red".
¬ ∀ y R(y) means "Not everything is red".
∃ y ¬ R(y) means "There is some non-red thing."
∃ y R(y) means "There is something that is red" or "There exists some red thing".
2.2.8 BDF
Let's examine a "Sillygism":
| Object-oriented is good. | |
| Ada is good. | |
| ∴ | Ada is Object-oriented. |
Very wrong! Better as a "Syllogism":
| Object-oriented is good. | |
| Ada is object-oriented. | |
| ∴ | Ada is good. |
That's right. In general:
- G(x) = x is good.
- O(x) = x is object-oriented.
| ∀ x (O(x) → G(x)) | |
| O(Ada) | |
| ∴ | G(Ada) |
A Well-Known Syllogism:
| All men are mortal. | |
| Socrates is a man. | |
| ∴ | Socrates is mortal. |
A Slightly Less Well-Known Syllogism:
- S(x) = x is a student of Discrete Mathematics.
- T(x) = x has taken Data Structures.
∀ x (S(x) → T(x))
Or more succinctly:
∀ x T(x)
(if the Domain of Discourse is decided on in advance to be "students in this class").
2.2.9 HJL
The Gospel as Domain of Discourse is an abundantly fruitful mindscape.
In his teachings, Paul the apostle uses conditionals (and their variations) and syllogistic reasoning a lot. For example: I Corinthians 15:29
Else what shall they do which are baptized for the dead, if the dead rise not at all? why are they then baptized for the dead?
All things that are done by people are done for a reason (i.e., they have a point). Baptisms for the dead are done by people. Therefore, baptisms for the dead have a point. If the dead rise not (i.e., there is no resurrection) then there would be no point to do baptisms for them. Thus, if baptisms for the dead have a point, then there is a resurrection of the dead. Therefore, the resurrection of the dead is real.
2.2.10 NPR
As a rule of thumb, universal quantifiers are followed by implications. For example, the symbolic form of "Every prime > 2 is odd" is
∀ x ((Prime(x) ∧ GreaterThanTwo(x)) → Odd(x))
or
∀ x > 2 (Prime(x) → Odd(x))
but not
∀ x > 2 (Prime(x) ∧ Odd(x)).
As a rule of thumb, existential quantifiers are followed by conjunctions. For example, the symbolic form of "There exists an even number that is prime" is
∃ x (Even(x) ∧ Prime(x)),
but not
∃ x (Even(x) → Prime(x)).
Remember to change the quantifier when negating a quantified proposition.
Take another example, the negation of the statement that "some cats like liver". It is not the statement that "some cats do not like liver"; it is that "no cats like liver," or that "all cats dislike liver." So with "cats" as the Universe of Discourse and letting L = "likes liver";
∃ x L(x) says "some cats like liver."
¬ ∃ x L(x) ≡ ∀ x ¬ L(x)
"All cats dislike liver", or "No cats like liver".
¬ ∀ x L(x)
"It is not the case that all cats like liver", or "Not all cats like liver".
¬ ∀ x ¬ L(x)
"Not all cats dislike liver", or "Some cats like liver".
2.2.11 TVX
There are two important concepts to keep in mind when dealing with predicates and quantifiers. To turn a first-order logic formula into a proposition, variables must be bound either by
- assigning them a value, or
- quantifying them.
What means Freedom Versus Bondage?
In formulas, variables can be free or bound. Bondage means being under the control of a particular quantifier. If φ is some Boolean formula and x is a variable in φ, then in both ∀ x (φ) and ∃ x (φ) the variable x is bound — free describes a variable in φ that is not so quantified.
As in propositional logic (AKA the propositional (or predicate) calculus), some predicate formulas are true, others false. It really depends on how its predicates and functions are interpreted. But if a formula has any free variables, in general its truth is indeterminable under any interpretation.
For example, let the symbol 'L' be interpreted as less-than. Whether the formula
∀ x L(x, y)
is true or not is indeterminable. But inserting an ∃ y right after the ∀ x makes it true. Yes, we just nested one quantifier inside another. And importantly, when nesting different-flavored quantifiers, the order in which they appear matters (but not if they are the same flavor).
Using a predicate, e.g., if (Q x y) is "x + y = x - y"
∀ x ∀ y (Q x y) is false;
∀ x ∃ y (Q x y) is true;
∃ x ∀ y (Q x y) is false; and
∃ x ∃ y (Q x y) is true.
2.3 GHI
"I hate that there are so many different ways to say the same thing," said Ila, her complainer imp feeling especially strong today.
Abu said, "I know what you mean. But I can see having more than one representation enhancing my understanding. Just as Feynman's knowledge of chemistry and physics enhanced his understanding and appreciation of flowers, so my puny discrete mathematical mind is enriched, not impoverished, by having more ways of seeing. I really am starting to see the beauty of it. The more representations, the clearer our understanding."
Ila replied, "Maybe, but I'm not convinced yet. Til, you no doubt agree with Abu, right?"
Til cautioned, "Yes, but we must be careful. Each representation has its own precision … and its own vagueness."
"How so?" asked Abu.
"We use words, symbols, pictures, etc., to understand our world and achieve mutual understanding amongst ourselves," said Til. "But each representation of an idea we seek to illuminate is just a facet of the whole, and subject to misinterpretation if solely focused on. We need to be holistic AND reductionistic, both — not one at the exclusion of the other."
Abu and Ila both looked mildly puzzled, but Til went on. "Look at how we write 1/2 versus ½ or \(\frac{1}{2}\). The first suggests one divided by two, the second or third the fraction one-half, what we get when we divide one by two. The process versus the result. Neither is more important than the other."
"Representational space deals with relations between ideas, concepts, aspects of reality. Representational fluency speaks to how nimbly we deal with aspects of reality like time and space, and our movement through each. Causality, cause and effect — three-dimensional spatial relationships, above, below, right, left, before or behind — proximity and locality, are you with me here?" said Til. He had noticed Ila starting to drift, although Abu was still focused.
Ila replied, "Yes, sorry. Could you explain more what you meant by, if there's any such thing as a central idea in math, representational fluency is it?"
"It's central," said Til, "because it's key to a mathematician's success. The successful ones work for and attain the ability to move fluently among various referent representations, while allowing a given representation to stand for different referents depending on the context. Especially when referring to functions, it's crucial to be able to move comfortably between equations, tables, graphs, verbal descriptions, etc."
| x | .05ex |
|---|---|
| 0 | 0.050 |
| 1 | 0.136 |
| 2 | 0.369 |
| 3 | 1.004 |
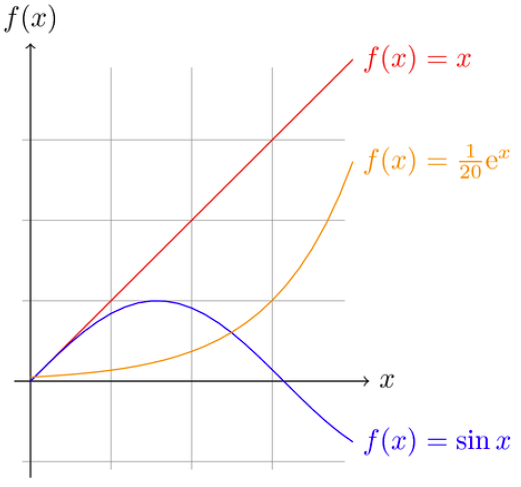
"Speaking of graphs," said Abu, "this picture you're showing us is what I've thought were graphs ever since I took algebra."
"Ila, do you agree this is the everyday ordinary meaning of graphs?" asked Til.
"Yes, except I know they're also these webby-looking things with dots and lines," said Ila. "Just another example of confusing terminology, this time using the same word to refer to two different things."
"Right, and we'll get to those types of graphs, important discrete structures as they are, later," said Til, ignoring her complaint. "But for now, here's what I want you to do. I've just sent to your pads a high-level summary of how mathematicians from Euclid (at least) on down work at the task of understanding. Take this list and find examples in math history of each step:"
- Think about how understanding will be assessed.
- Decide that an important measure of understanding is easy, fluid translation (movement) between representations.
- Make in-the-large pattern recognition easier because of fluency of representations. (Expert mathematicians perceive big, meaningful patterns. Novices see little, not so meaningful patterns.)
- Gain expertise by lots of problem solving practice.
- Evolve representations via problem solving practice.
- Introduce, test and refine representations in this evolutionary process.
Nurture evolving representations as they grow progressively more sophisticated.
-~-~-~-~-~-
2.3.1 ZBD
How have mathematicians generalized functions? They defined relations. With one big difference, relations are essentially functions. The difference is, there is no "fan-out" constraint on relations as there is on functions. What that means is that an element of the domain of a relation can map to any number of (zero, one or more) elements in its codomain.
VTO: A binary relation R from a set A to a set B is a subset: R ⊆ A × B. A binary relation R on a set A (a self relation) is a subset of A × A, or a relation from A to A (from the set to itself).
VTO: A × B, the Cartesian product (or just product) of set A with set B is the set of all ordered pairs (a b) where a ∈ A and b ∈ B. This generalizes to n sets in the obvious way.
For an A × B example:
- A = [a b c]
- B = [1 2 3]
- R = [(a 1) (a 2) (b 2) (b 3) (c 3)]
For a self relation example:
- A = [a b c]
- R = [(a a) (a b) (a c)]
2.3.2 FHJ
VTO: extravaganza of special properties of binary relations — given:
- A Universe U
- A binary relation R on a subset of U
- A shorthand notation xRy for "x is related to y" — shorter than saying "the pair (x y) is in the relation R" (in symbols, (x y) ∈ R), and shorter too than "x is related to y (under the relation R)". Since "(under the relation R)" is the assumed context, choose succinctness.
R is reflexive iff ∀ x [x ∈ U → xRx].
If U = ∅ then the implication is vacuously true — so the void relation on a void Universe is reflexive. Reflect on that. If U is not void, then to be a reflexive relation, all elements in the subset of U must be present.
R is symmetric iff ∀ x ∀ y [xRy → yRx].
R is antisymmetric iff ∀ x ∀ y [xRy ∧ yRx → x = y].
From this definition, using logic, you should be able to show that if xRy and x ≠ y then it is false that yRx.
R is transitive iff ∀ x ∀ y ∀ z [xRy ∧ yRz → xRz].
2.3.3 LNP
CSP naturally, binary relations readily generalize to n-ary relations.
2.3.4 RTV
CSP a very brief treatment of equivalence relations.
2.3.5 XZB
To end this foray into all things relational, it is illuminating to investigate how mathematicians think and make sense of the world. However, this investigation will be limited for now to one mathematician in particular — Roger Penrose.
So this is how one world-class mathematician (who is also a mathematical physicist) thinks. In this excerpt from his book The Large, the Small and the Human Mind, with abundant intellectual humility, Penrose writes:
What is consciousness?
Well, I don't know how to define it.
I think this is not the moment to attempt to define consciousness, since we do not know what it is. I believe that it is a physically accessible concept; yet, to define it would probably be to define the wrong thing. I am, however, going to describe it, to some degree. It seems to me that there are at least two different aspects to consciousness. On the one hand, there are passive manifestations of consciousness, which involve awareness. I use this category to include things like perceptions of colour, of harmonies, the use of memory, and so on. On the other hand, there are its active manifestations, which involve concepts like free will and the carrying out of actions under our free will. The use of such terms reflects different aspects of our consciousness.
I shall concentrate here mainly on something else which involves consciousness in an essential way. It is different from both passive and active aspects of consciousness, and perhaps is something somewhere in between. I refer to the use of the term understanding, or perhaps insight, which is often a better word. I am not going to define these terms either — I don't know what they mean. There are two other words I do not understand — awareness and intelligence. Well, why am I talking about things when I do not know what they really mean? It is probably because I am a mathematician and mathematicians do not mind so much about that sort of thing.
They do not need precise definitions of the things they are talking about, provided they can say something about the connections between them.
The first key point here is that it seems to me that intelligence is something which requires understanding. To use the term intelligence in a context in which we deny that any understanding is present seems to me to be unreasonable. Likewise, understanding without any awareness is also a bit of nonsense. Understanding requires some sort of awareness. That is the second key point. So, that means that intelligence requires awareness. Although I am not defining any of these terms, it seems to me to be reasonable to insist upon these relations between them.
3 TWO
"So, what is the connection between probability and counting?" asked Til. Ila stared with wonder and amazement. It was like Til had no problem whatsoever dispensing with the normal pleasantries of conversation. Like that time when she arrived a few minutes before Abu and tried to make small talk with Til. "So, it seems that you're interested in stars!" she had said. "Yes, I am." Til had replied, and then got that faraway look in his eyes, like he was suddenly out there among the stars, abruptly leaving the nearby flesh-and-blood human behind.
Like he had that time by arriving with a cheery greeting, Abu broke the awkward silence this time by cautiously saying "Well, I think it has to do with counting the number of ways something can happen and then confirming that count by experimenting, like flipping a coin or rolling dice."
"Ah, so you're a frequentist!" said Til. Abu blinked and then quickly nodded, alert to the agitation he sensed well up in Ila. "Wait, what's a frequentist? said Ila. "As opposed to a subjectivist, whose view of probability is different," said Til.
"Let me compare and contrast these two schools of thought," said Til, after a brief pause while he gathered his thoughts and Abu and Ila sat lost in theirs. "To a frequentist, probability is counting the number of times something actually happens, like landing heads to use Abu's coin flipping experiment, and comparing that frequency with the number of flips. The 'landing heads' when flipping a coin is called an event, the 'landing-either-heads-or-tails (but not neither and certainly not both)' is called the space of possibilities, or the probability space of this experiment. In other words, the probability space is all possible outcomes, and the event is a subset of that space. The frequentist holds that the frequency of actual outcomes, counting say 51 heads in 100 coin tosses, is an approximation to the exact probability of getting heads on any single toss of a coin."
"So, if I understand this right," said Ila, "I can say the probability of getting heads is 51/100, or 498/1000 or whatever it is after repeating the experiment however many times I want." "Yes, if you're a frequentist!" said Til. "But I really just want to say it's 50%, or a 50-50 chance, because of how coins have two sides, and unless there's something funny about my quarter here, tossing it gives no preference to one side or the other. So either is equally likely, right?" "So right, if you're a thought-experiment frequentist!" said Til.
"But aren't there fake coins that are biased to land more often heads than tails, or vice-versa?" said Abu. "Yes, but what's your point?" said Til. "Well, if I did the experiment of tossing some such biased coin a thousand times, and counted 600 heads," said Abu, "I'd be more inclined to suspect the coin was unfair than to think the likelihood of getting heads was 60%." "That's because you have a high degree of belief, a subjective intuition if you will, about how coins should behave." said Til.
"Is that what a subjectivist is, someone who treats probability as a subjective belief in how likely something is?" said Ila. "Exactly right!" said Til. "Obviously, frequentism cannot work in all cases, because some 'experiments' can't be done, or if not outright impossible, can't be repeated, or even tried once without disastrous results." Abu chimed in, "Like what's the probability that the world will end and humanity extinguish itself in a nuclear holocaust? I may think it's not very likely, but someone else might disagree and think the probability is high."
"I've got one!" said Ila. "What's the probability that our sun will go supernova tomorrow?"
"I'd give that one a 0% chance, personally," said Abu. "Same here," said Til. "But that's just our belief — mixed of course with scientific knowledge about how stars live and die. When people use pseudoscience to predict the future, or substitute opinion for fact, and 'estimate' probabilities to further some hidden agenda — that's when math abuse, and truth abuse abound."
"Truth abuse sounds worse than math abuse," said Ila. "Truth is," replied Til, "popular culture conspires to disguise truth, and substitute illusion for what's real. For example, take the famous Mr. Spock from Star Trek. In the original series, Spock was always telling Captain Kirk 'I estimate our chances (of getting out of such-and-such predicament) to be 0.02794%' or some such ridiculously small and precise number. And viewers accepted this ludicrous scenario without question because Hollywood had convinced them Mr. Spock was this logical, mathematical, scientific paragon."
Again, Abu and Ila paused to consider the implications of what Til had just said. Ila had a thought. "Til, are you a frequentist or a subjectivist?" she asked. "Both!" said Til, with a mischievous smile. Then while softly clearing his throat he subvocalized the contradictory addendum, "And neither."
"At any rate," continued Til, full voice, "if we're going to learn how to count today we'd better get to it!"
-~-~-~-~-~-
3.1 JKL
Basic Counting
Here are two TLAs sharing Elementary and Combinatorics (the study of counting, or of how things combine):
- EEC (Elementary Enumerative Combinatorics) — treated lightly.
- EGC (Elementary Generative Combinatorics) — mentioned here by way of contrast. Delved into deeper when we get to trees.
3.1.1 DFH
Counting involves applying logic and some general principles to find the number of ways some choice can be made, some task can be done, or some event can happen. Counting ways of combining abstract or concrete objects from given sets they belong to is the goal.
VTO:
The Addition Principle (AKA the Sum Rule): faced with a task to select just one member from each set in a collection of two or more sets, the number of ways to make the selection is the sum of the sizes of the sets, provided the sets have no members in common.
Example: The number of ways to choose one vowel or one consonant from the alphabet is 5 + 21 = 26. It should not be surprising that this is the same as the number of ways to choose one letter from the whole alphabet. The Addition Principle involves an either-or choice, where the choices are mutually exclusive.
VTO:
The Multiplication Principle (AKA the Product Rule): faced with a task to select one member from one set, and one member from another set, and (continue with arbitrarily many sets) …, the number of ways to do so is the product of the sizes of the sets. Here again it is usually stipulated that the sets are disjoint — meaning they have no members in common.
Example: The number of ways to choose one vowel and one consonant from the alphabet is \(5 \cdot 21 = 105\). The Multiplication Principle involves a both-and choice.
In sum, adding is like or-ing, and multiplying is like and-ing, to liken '+' to ∨ and '*' to ∧.
Mixing these two principles in certain ways leads to basic counting techniques applicable to many many counting tasks. The hard part of the solution to any counting problem is choosing the appropriate model and technique. After that, applying the appropriate technique (formula) is easy.
VTO:
A permutation is an arrangement, where order matters (just like with nested quantifiers).
A combination is a subset, where order matters not, like with sets in general.
So whether order matters or not is one dimension of a counting problem, with another dimension being whether or not repetition of elements is allowed. Generally speaking these considerations are germane to either permutations or combinations, but there are subtle variations of permunations and combitations to take into account as well.
To wit, given a set of n objects, say you want to select r of them. After choosing one object from the set —
- you can either put it back — called selection with replacement (or allowing repetition)
- or not — called selection without replacement (or disallowing repetition)
Choosing the appropriate technique requires answering the two questions:
- Does the order of the selected objects matter or not?
- Is the selection with or without replacement (repetition)?
In general, how many different possible sequences (arrangements) of objects there are depends on the size (length) of the sequence. Selection without replacement of r objects from a set of n objects naturally constrains r to be at most n. If more than one object is selected (\(r \ge 2\)), two different orderings or arrangements of the objects constitute different permutations. Thus it is:
- Choose the first object n ways, and
- Choose the second object \((n - 1)\) ways (when selection is without replacement, there is one fewer object to choose from) and
- Choose the third object \((n - 2)\) ways (again without replacement,) …
Finally choose the \(r^{th}\) object \((n - r + 1)\) ways.
By the Multiplication Principle, the number of r-permutations of n things, or said another way, the number of permutations of n things taken r at a time is
\(P(n, r) = n(n - 1)(n - 2) \cdots (n - r + 1) = n!/(n - r)!\)
If selection is without replacement but order does not matter, this is the same as selecting subsets of size r from a set of size n. Again, \(0 \le r \le n\). The secret is to divide out the number of arrangements or permutations of the r objects from the set of permutations of n objects taken r at a time. Since each r-combination can be arranged \(r!\) ways, we have \(r!\) permutations for each r-combination. So the number of r-combinations of n things, or, the number of combinations of n things taken r at a time is
\(C(n, r) = P(n, r)/P(r, r) = \frac{n!}{(n - r)! r!}\)
Example: How many ways can we choose a three-letter subset of the nine letters ABCDELMNO?
We have selection without replacement, and because we want a subset (not a sequence) the order does not matter — CDE = CED = DCE = DEC = ECD = EDC — they're all the same. So n = 9 and r = 3:
\(C(9, 3) = \frac{9!}{(9 - 3)! 3!} = \frac{9!}{6!3!} = \frac{362880}{720 \cdot 6} = 84\)
3.1.2 JLN
Basic Probability Theory
Taking a frequentist position is the usual way to begin exploring the vast space of BPT.
VTO:
A Probability Space is a finite set of points, each of which represents one possible outcome of an experiment. This is the discrete definition, as opposed to the continuous one with infinite points.
- Each point x is associated with a real number between 0 and 1 called the probability of x.
- The sum of all the points' probabilities \(= 1\).
- Given n points, if all are equally likely (a typical assumption) then \(1/n\) is the probability of each point.
Example: What are the possible outcomes of throwing a single fair die?
[1 2 3 4 5 6] is the probability space of outcomes as a lisp
vector.
VTO:
An Event is a subset of the points in a probability space.
- P(E) (or Pr(E), or sometimes even p(E)) denotes the probability of the event E.
- If the points are equally likely, then P(E) is the sum of the points in E divided by the sum of the points in the entire probability space.
In the (fair) die throwing example, each number 1-6 is equally likely, so 1/6 is the probability of each number.
Example: What are the possible outcomes of flipping two fair coins?
- Probability Space: 4 outcomes (1/4 probability of each outcome).
- Event: seeing a head (
H) and a tail (T) — the middle two of the four possibilities:HHHTTHTT
There are two points in the event, so 2/4 or 1/2 is the event's probability.
Ramp Up to Four
When flipping four coins is the experiment, the probability space quadruples:
- Probability Space: 16 outcomes, each having 1/16 probability.
Double Previous Event
Event: seeing two heads and two tails.
HHHHHHHTHHTHHHTTHTHHHTHTHTTHHTTTTHHHTHHTTHTHTHTTTTHHTTHTTTTHTTTT
With 6 points in it (can you pick them out?) 6/16 or 3/8 is the probability of this event.
3.2 MNO
"Euclid proved there are infinitely many primes. Can you?!" Til said. His words were met with utter silence. Dropping that bombshell meant his two pupils had to readjust to the darkness of uncertainty while trying to process what Til just said so nonchalantly. Without waiting for the daze to subside, he went on. "Before the end of today's session, you will have learned the classic method he used to accomplish this amazing feat."
"Another way to say there are infinitely many primes is to say there is no largest prime," said Til. "Suppose not …" he trailed off, pausing for dramatic effect.
"Wait, what do you mean, suppose not?" said Ila. "I thought we were trying to prove a negative anyway, that there is no largest prime?"
"What I mean is, suppose, in contradiction to what we seek to establish, that there is a largest prime. Call it x."
"Hold on," said Ila. "I don't see how that helps us prove that there is no largest prime?"
"What we're going to do is show that it is logically impossible for this x, this so-called largest prime to exist!" said Til.
Abu chimed in. "This sounds like some Latin phrase I read somewhere — I believe it's reductio ad absurdum — RAA to TLA it."
Til replied, "Right As Always!" To which Ila takes umbrage. "Hey, Abu's not always right. I'm right too sometimes."
"I was just kidding," said Til. "But you realize that saying Abu is always right says nothing about how often you're right, right?"
"I know," said Ila. "It's just that he's always so smiley and self-assured and smug. Like this stuff is a piece of cake to him."
"Hey, it is a piece of cake — and a delicious one at that!" said Abu.
"Can we get on with the proof?" said Til. Both Ila and Abu nodded yes, Abu still grinning — bad enough, thought Ila, but worse still, he winked at me as Til looked down at his pads. Grrr!
"So, x is the greatest prime. Now follow these seven steps," said Til.
- "First form the product of all primes less than or equal to x, and then add 1 to the product.
- This yields a new number y. To concretize, y = (2 × 3 × 5 × 7 × … × x) + 1.
- If y is itself a prime, then x is not the greatest prime, for y is obviously greater than x.
- If y is composite (i.e., not a prime), then again x is not the greatest prime. That's because being composite means y must have a prime divisor z; and z must be different from each of the primes 2, 3, 5, 7, …, up to x. Hence z must be a prime greater than x.
- But y is either prime or composite, there's no third option.
- Hence x is not the greatest prime.
- Hence there is no greatest prime."
"Whoa, back up, please!" said Ila. "I'm doing this and I don't see where y is ever composite:"
- 2 + 1 = 3
- 2 × 3 + 1 = 7
- 2 × 3 × 5 + 1 = 31
- 2 × 3 × 5 × 7 + 1 = 211
- 2 × 3 × 5 × 7 × 11 + 1 = 2311
"All of these, 3, 7, 31, 211, 2311, … are prime," said Ila. "Abu, don't you agree?"
"Well, actually, look at the very next one in the sequence." said Abu. "2 × 3 × 5 × 7 × 11 × 13 + 1 = 30031, which is 59 (prime) × 509 (also prime), if I calculate correctly."
Ila was completely taken aback. Why she didn't think to go one step further caused her jaw to drop with a thud.
Noticing Ila's nonplussitude, Til reassured her. "Abu calculated correctly, but you would have too, and the fact you stopped one short is just another testimony to the all too human tendency to leap to conclusions with inductive assertions."
"So, yeah, I see it now," said Ila, recovering. "That special number y — made by adding 1 to the product of all primes in a supposedly complete list of primes — always gives rise, one way or another, to a prime not in the list!"
"You got it!" said Til. "Me too," grinned Abu. "It's a weird way to prove something, though. It just seems backwards."
"It is backwards," said Til. "It's called proof by contradiction, or reducing to the absurd, to translate your Latin phrase. It's a wonderfully respectable, nay, even venerable, proof technique."
"Right!" said Ila. "After all, it goes all the way back to Euclid!"
3.2.1 PRT
Til's aside, we fire our opening salvo into "mathmagic land" by way of distinguishing Elementary Number Theory from Advanced (or Analytic) Number Theory (ANT)). ANT uses the techniques of calculus to analyze whole numbers, whereas ENT uses only arithmetic and algebra. What more primordial concept to begin with than those multiplicative building blocks, the atoms of numbers, primes. Let's examine several ways to say the same thing:
VTO: a prime is a number (integer) greater than 1 that is divisible only by 1 and itself.
- A prime is a positive integer > 1 with exactly 2 divisors (those being 1 and itself).
- A positive integer > 1 that is not prime is called composite.
- In first-order logic, prime(n) ↔ ∀ x ∀ y [(x > 1 ∧ y > 1) → xy ≠ n].
- A composite is a positive integer with 3 or more divisors (because 3 is the first number greater than 2, and a number cannot have fewer than two divisors).
- 1 is neither prime nor composite — call it unit.
- 2 is the only even prime: ∃ ! n [even(n) ∧ prime(n)]. The "∃ !" construct is short for "there exists a unique" or "there exists one and only one".
3.2.2 VXZ
What's so important about primes?
The Fundamental Theorem of Arithmetic, that's what. The FTA says that every positive integer can be written as the product of prime numbers in essentially one way. (So, 2 × 2 × 2 × 3 × 5 × 7 = 840 = 7 × 5 × 3 × 2 × 2 × 2 is two ways in one — the order of the factors doesn't matter.)
Sometimes uniqueness is guaranteed by phrasing it as "every integer greater than 1 can be written uniquely as a prime or as the product of two or more primes where the prime factors are written in order of nondecreasing size". But what about 1? The first statement didn't exclude it, why did the second?
Determining if a given integer is prime is a key component to modern cryptology — and crucial to the success of the enterprise of cryptology is the difficulty of factoring large integers into their prime factors.
More prime lore can be perused and pursued by the interested reader, but here's a playful smattering:
- What's the smallest three-digit number that remains prime no matter how its digits are shuffled?
- Why are the primes 2, 5, 71, 369119, and 415074643 so special?
- Cicadas of the genus Magicada appear once every 7, 13, or 17 years; whether it's a coincidence or not that these are prime numbers is unknown.
- Sherk's conjecture. The nth prime, if n is even, can be represented by the addition and subtraction of 1 with all the smaller primes. For example, 13 = 1 + 2 - 3 - 5 + 7 + 11.
- You look up one on your own so sexy can be 6 (because the Latin for six is sex).
- Sexy primes are such that n and n + 6 are both prime. The first few such pairs are 5-11, 11-17, and 13-19.
3.2.3 ADG
There are many more prime puzzles for our pondering pleasure provided also courtesy David Wells. A random sample will suffice for now.
Is there a prime between n and 2n for every integer n > 1? Yes, provably so.
Is there a prime between n2 and (n + 1)2 for every n > 0? No one knows.
Many primes are of the form n2 + 1 (e.g., 2, 5, 17, 37, 101, …). Are there a finite or infinite number of primes of this form? No one knows.
Is there an even number greater than 2 that is not the sum of two primes? No one knows. (That there is not is Goldbach's Conjecture.)
Is there a polynomial with integer coefficients (e.g., n2 - n + 41) that takes on only prime values at the integers? The next exercise explores this question.
3.2.4 JMP
One very special kind of prime is the so-called Mersenne prime, which is one of the form 2p - 1 where p is prime. Here are a few examples:
- 22 - 1 = 3
- 23 - 1 = 7
- 25 - 1 = 31
- 27 - 1 = 127
- 211 - 1 = 2047 = 23 × 89 — ∴ not prime.
- …
- 231 - 1 = 2147483647 (prime or not? How do you tell, easily?)
- …
The Great Internet Mersenne Prime Search (GIMPS) can be googled to examine the 48th known Mersenne prime, a number with over 17 million digits (do not even THINK about looking at them all).
3.2.5 SVY
How many primes are there up to a given number n? The Prime Number Theorem reveals in a sense how the primes are distributed among the composites. But how does one define a function that measures the distribution of prime numbers?
VTO: Define the function π(n) as the number of primes not exceeding (less than or equal to) the number n. Check it out:
| n | π(n) | n / π(n) | ⌈ n / log n ⌉ |
|---|---|---|---|
| 10 | 4 | 2.5 | 5 |
| 100 | 25 | 4.0 | 22 |
| 1000 | 168 | 6.0 | 145 |
| 10,000 | 1,229 | 8.1 | 1,086 |
| 100,000 | 9,592 | 10.4 | 8,686 |
| 1,000,000 | 78,498 | 12.7 | 72,383 |
| 10,000,000 | 664,579 | 15.0 | 620,421 |
| 100,000,000 | 5,761,455 | 17.4 | 5,428,682 |
| 1,000,000,000 | 50,847,534 | 19.7 | 48,254,943 |
| 10,000,000,000 | 455,052,512 | 22.0 | 434,294,482 |
This seems to show that \(\pi(n) \approx \frac{n}{\log n}\).
More formally, \(\lim_{n \rightarrow \infty} \frac{\pi(n)}{(n\ / \log n)} = 1\).
The discovery of [this theorem] can be traced as far back as Gauss, at age fifteen (around 1792), but the rigorous mathematical proof dates from 1896 and the independent work of C. de la Vallée Poussin and Jacques Hadamard. Here is order extracted from confusion, providing a moral lesson on how individual eccentricities can exist side by side with law and order.
— from The Mathematical Experience by Philip J. Davis and Reuben Hersh.
So \(n\ / \log n\) is a fairly simple approximation for \(\pi(n)\), but it is not especially close. Much closer is an approximation that uses the renowned Riemann zeta function:
\(\zeta(z) = 1 + \frac{1}{2^z} + \frac{1}{3^z} + \frac{1}{4^z} + \cdots\)
\(R(n) = 1 + \sum_{k = 1}^{\infty} \frac{1}{k\zeta(k + 1)} \frac{(\log n)^k}{k!}\)
Let's see how much better R(n) approximates π(n):
| n | π(n) | R(n) |
|---|---|---|
| 100,000,000 | 5,761,455 | 5,761,552 |
| 200,000,000 | 11,078,937 | 11,079,090 |
| 300,000,000 | 16,252,325 | 16,252,355 |
| 400,000,000 | 21,336,326 | 21,336,185 |
| 500,000,000 | 26,355,867 | 26,355,517 |
| 600,000,000 | 31,324,703 | 31,324,622 |
| 700,000,000 | 36,252,931 | 36,252,719 |
| 800,000,000 | 41,146,179 | 41,146,248 |
| 900,000,000 | 46,009,215 | 46,009,949 |
| 1,000,000,000 | 50,847,534 | 50,847,455 |
3.2.6 BEH
There is an astounding proof that there exist arbitrarily long sequences of highly composite consecutive integers! (That means having as many prime factors as we want.) In other more precise words:
Let r and n be positive integers. Then there exist r consecutive numbers, each divisible by at least n distinct primes.
Actually, we would need a little more knowledge before looking at the proof of this amazing (if you think about it) theorem. But as persistent investigation will reveal, what this proof demonstrates (like others) is that these multiplicative building blocks called the prime numbers have a gamut of surprises.
3.2.7 KNQ
Concepts known to ancient Greek mathematicians and no doubt before then too, Greatest Common Divisors (GCD) and Least Common Multiples (LCM) have an interesting interplay.
VTO: In lisp style, the Greatest Common Divisor (gcd a b) is the
largest integer that divides both a and b, and its
counterpart, the Least Common Multiple (lcm a b), is the
smallest positive integer that is divisible by both a and
b. Integers whose gcd is 1 are called coprime (or relatively
prime), while pairwise coprime (or pairwise relatively prime)
describes a set of integers every pair of which is coprime.
3.2.8 TWZ
Six more topics and then we'll be ready to practice all this number theory:
- Alternate Base Representation
- The Division Theorem
- Modular Arithmetic
- Modular Multiplicative Inverse
- Modular Exponentiation
- Euclidean GCD, plain versus extended
Infinite Representational Fluency. Sounds crazy, no? But representations of integers are endless, because the choice of base to use is infinite.
- Alternate Base Number Representation
- n = (ak ak-1 … a1 a0)b
| b | Name for ABR | Example n = (expanding above form making b explicit) |
|---|---|---|
| 2 | binary | a6 26 + a5 25 + a4 24 + a3 23 + a2 22 + a1 21 + a0 20 |
| 3 | ternary | a5 35 + a4 34 + a3 33 + a2 32 + a1 31 + a0 30 |
| 8 | octal | a4 84 + a3 83 + a2 82 + a1 81 + a0 80 |
| 16 | hexadecimal | a2 162 + a1 161 + a0 160 |
| 64 | base-64 (imagine that) | a2 642 + a1 641 + a0 640 |
And so forth, ad infinitum.
- Algorithm for Alternate Base Representations
- Repeat the three steps until zero appears on the left side of the equation
n = … + a6 b6 + a5 b5 + a4 b4 + a3 b3 + a2 b2 + a1 b1 + a0 b0.
- The right-most ai is the remainder of the division by b.
- Subtract this remainder from n.
- Divide both sides of the equation by b.
Each iteration yields one ai coefficient. Simple algebra guarantees the correctness of this algorithm.
For example, take n =97 and b = 3.
| 97 | = | a4 × 34 + a3 × 33 + a2 × 32 + a1 × 31 + a0 × 30 | |
| 1) | 97/3 | = | 32, remainder = 1 = a0 |
| 2) | 96 | = | a4 × 34 + a3 × 33 + a2 × 32 + a1 × 31 |
| 3) | 32 | = | a4 × 33 + a3 × 32 + a2 × 31 + a1 × 30 |
| 1) | 32/3 | = | 10, remainder = 2 = a1 |
| 2) | 30 | = | a4 × 33 + a3 × 32 + a2 × 31 |
| 3) | 10 | = | a4 × 32 + a3 × 31 + a2 × 30 |
| 1) | 10/3 | = | 3, remainder = 1 = a2 |
| 2) | 9 | = | a4 × 32 + a3 × 31 |
| 3) | 3 | = | a4 × 31 + a3 × 30 |
| 1) | 3/3 | = | 1, remainder = 0 = a3 |
| 2,3) | 3 | = | a4 × 31, 1 = a4 × 30 |
| 1) | 1/3 | = | 0, remainder = 1 = a4 |
| 2,3) | 0 | = | 0, so |
| 97 | = | 1 × 34 + 0 × 33 + 1 × 32 + 2 × 31 + 1 × 30 | |
| = | 81 + 9 + 6 + 1 = 97, ∴ 9710 = 101213 |
3.2.9 CFI
CSP The Division Theorem
3.2.10 LOR
CSP Modular Arithmetic
3.2.11 UXA
CSP Modular Multiplicative Inverse (MMI)
3.2.12 DGJ
Modular Exponentiation: as powerful as simple as algorithms go.
Say we want to compute, for example, 8932753%4721. (Why we would want to do that is a mystery, but let it go for now.)
Doing this the straightforward way — raising 893 to the power 2753 and then reducing that huge number modulo 4721 — is difficult and slow to do by hand. An easy, fast way to do it (by hand and even faster by computer) first expands the exponent in base 2:
2753 = 1010110000012 = 1 + 26 + 27 + 29 + 211 = 1 + 64 + 128 + 512 + 2048
In this table of powers of 2 powers of 893, all instances of ≡ should technically be ≡4721, as all intermediate values are reduced modulo 4721:
| 8931 | ≡ | 893 | ||
| 8932 | ≡ | 4321 | ||
| 8934 | ≡ | 43212 | ≡ | 4207 |
| 8938 | ≡ | 42072 | ≡ | 4541 |
| 89316 | ≡ | 45412 | ≡ | 4074 |
| 89332 | ≡ | 40742 | ≡ | 3161 |
| 89364 | ≡ | 31612 | ≡ | 2285 |
| 893128 | ≡ | 22852 | ≡ | 4520 |
| 893256 | ≡ | 45202 | ≡ | 2633 |
| 893512 | ≡ | 26332 | ≡ | 2261 |
| 8931024 | ≡ | 22612 | ≡ | 3999 |
| 8932048 | ≡ | 39992 | ≡ | 1974 |
We can then exploit this table of powers of 893 to quickly compute 8932753%4721:
| ≡ | 8931 + 64 + 128 + 512 + 2048 |
| ≡ | 893(1 + 64 + 128 + 512 + 2048) |
| ≡ | 8931 ⋅ 89364 ⋅ 893128 ⋅ 893512 ⋅ 8932048 |
| ≡ | 893 ⋅ 2285 ⋅ 4520 ⋅ 2261 ⋅ 1974 |
| ≡ | 1033 ⋅ 4520 ⋅ 2261 ⋅ 1974 |
| ≡ | 91 ⋅ 2261 ⋅ 1974 |
| ≡ | 2748 ⋅ 1974 |
| ≡ | 123 |
| = | 123 |
3.2.13 MPS
- Euclidean GCD Algorithm
- one for the book!
Euclid's famous algorithm to find the GCD of two numbers (positive integers) goes like this. Divide the larger number by the smaller, replace the larger by the smaller and the smaller by the remainder of this division, and repeat this process until the remainder is 0. At that point, the smaller number is the greatest common divisor.
3.2.14 VYB
CSP the Extended Euclidean GCD algorithm.
3.3 PQR
"Solving a system of simultaneous congruences is what we're going to tackle today," said Til, synching his pad to Abu's and Ila's.
"Let's say we're given three congruences, which I've numbered
1-3. This seeds our knowledge base with facts about an unknown
quantity x that we want to solve for. We'll use helper variables
t, u, and v; some basic facts about congruences modulo m
(that you two will verify); and some eyeballing of modular inverses
— altogether, 31 Facts of arithmetic and algebra. We'll record
how we arrive at each fact that follows from previous facts."
| Fact # | Fact Description | How Arrived At? |
|---|---|---|
| 1. | \(x\ \equiv_7\ 4\) (equivalently, \(x\ \%\ 7 = 4)\). | Given congruence. |
| 2. | \(x\ \equiv_{11}\ 2\) (equivalently, \(x\ \%\ 11 = 2)\). | Given congruence. |
| 3. | \(x\ \equiv_{13}\ 9\) (equivalently, \(x\ \%\ 13 = 9)\). | Given congruence. |
| 4. | If \(a\ \equiv_m\ b\) then \(a = mk + b\) for some \(k\). | By definition of \(\equiv_m\). |
| 5. | If \(a\ \equiv_m\ b\) then \(a + c\ \equiv_m\ b + c\). | Easily verified by Ila. |
| 6. | If \(a\ \equiv_m\ b\) then \(a - c\ \equiv_m\ b - c\). | Easily verified by Ila. |
| 7. | If \(a\ \equiv_m\ b\) then \(ac\ \equiv_m\ bc\). | Easily verified by Ila. |
| 8. | If \(a\ \equiv_m\ b\) then \(a\ \equiv_m\ b\ \%\ m\) and \(a\ \%\ m\ \equiv_m\ b\). | Easily verified by Abu. |
| 9. | If \(a\ \equiv_m\ b\) then \(a\ \equiv_m\ b + m\). | Easily verified by Abu. |
| 10. | \(x = 7t + 4\) | Fact 1 used with Fact 4. |
| 11. | \(7t + 4\ \equiv_{11}\ 2\) | Fact 10 substituted into Fact 2. |
| 12. | \(7t\ \equiv_{11}\ -2\) | Fact 6 used to subtract 4 from both sides of Fact 11. |
| 13. | \(7t\ \equiv_{11}\ 9\) | Fact 9 used to add 11 to the RHS of Fact 12. |
| 14. | Need to find an MMI mod 11 of 7. | Looked for a multiple of 7 that is 1 more than a multiple of 11. |
| 15. | \(8 \times 7 = 56 = 1 + 5 \times 11\). | Eyeballed it. So 8 is TUMMI mod 11 of 7. |
| 16. | \(56t\ \equiv_{11}\ 72\) | Used Fact 7 to multiply both sides of Fact 13 by 8 from Fact 15. |
| 17. | \(t\ \equiv_{11}\ 6\) | Used Fact 8 twice with \(m = 11; 56\ \%\ 11 = 1; 72\ \%\ 11 = 6\). |
| 18. | \(t = 11u + 6\) | Used Fact 4 applied to Fact 17. |
| 19. | \(x = 7(11u + 6) + 4 = 77u + 46\) | Substituted Fact 18 into Fact 10 and simplified. |
| 20. | \(77u + 46\ \equiv_{13}\ 9\) | Substituted Fact 19 into Fact 3. |
| 21. | \(12u + 7\ \equiv_{13}\ 9\) | Used Fact 8 with \(m = 13; 77\ \%\ 13 = 12, 46\ \%\ 13 = 7\). |
| 22. | \(12u\ \equiv_{13}\ 2\) | Used Fact 6 to subtract 7 from both sides of Fact 21. |
| 23. | Need to find an MMI mod 13 of 12 | Looked for a multiple of 12 that is 1 more than a multiple of 13. |
| 24. | \(12 \times 12 = 144 = 1 + 11 \times 13\) | Eyeballed it. So 12 is TUMMI mod 13 of 12. |
| 25. | \(u\ \equiv_{13}\ 24\) | Used Fact 7 to multiply both sides of Fact 22 by 12 from Fact 24. |
| 26. | \(u\ \equiv_{13}\ 11\) | Used Fact 8 with \(m = 13; 24\ \%\ 13 = 11\). |
| 27. | \(u = 13v + 11\) | Used Fact 4 applied to Fact 26. |
| 28. | \(x = 77(13v + 11) + 46\) | Substituted Fact 27 into Fact 18. |
| 29. | \(x = 1001v + 893\) | Simplified Fact 28. |
| 30. | \(x\ \equiv_{1001} 893\) | Reverse-applied Fact 8 to Fact 29. |
| 31. | \(x = 893\) is the simultaneous solution. | Double-checked: 893 % 7 = 4, 893 % 11 = 2, 893 % 13 = 9. |
"Why must 893 necessarily be the solution?" asked Abu. Til answered, "Examine this next table and arrive at your own conclusions. We're out of time for today."
| N | N % 3 | N % 5 | N % 8 | N % 4 | N % 6 |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 | 1 | 1 |
| 2 | 2 | 2 | 2 | 2 | 2 |
| 3 | 0 | 3 | 3 | 3 | 3 |
| 4 | 1 | 4 | 4 | 0 | 4 |
| 5 | 2 | 0 | 5 | 1 | 5 |
| 6 | 0 | 1 | 6 | 2 | 0 |
| 7 | 1 | 2 | 7 | 3 | 1 |
| 8 | 2 | 3 | 0 | 0 | 2 |
| 9 | 0 | 4 | 1 | 1 | 3 |
| 10 | 1 | 0 | 2 | 2 | 4 |
| 11 | 2 | 1 | 3 | 3 | 5 |
| 12 | 0 | 2 | 4 | 0 | 0 |
| 13 | 1 | 3 | 5 | 1 | 1 |
| 14 | 2 | 4 | 6 | 2 | 2 |
| 15 | 0 | 0 | 7 | 3 | 3 |
| 16 | 1 | 1 | 0 | 0 | 4 |
| 17 | 2 | 2 | 1 | 1 | 5 |
| 18 | 0 | 3 | 2 | 2 | 0 |
| 19 | 1 | 4 | 3 | 3 | 1 |
| 20 | 2 | 0 | 4 | 0 | 2 |
| 21 | 0 | 1 | 5 | 1 | 3 |
| 22 | 1 | 2 | 6 | 2 | 4 |
| 23 | 2 | 3 | 7 | 3 | 5 |
| 24 | 0 | 4 | 0 | 0 | 0 |
3.3.1 EHK
The mystery puzzle (exercise) should throw some light on the table just seen.
3.3.2 NQT
We have been investigating a modular arithmetic scenario known to the first century Chinese and probably before that too. But the name has stuck to them: the Chinese Remainder Theorem. In a nutshell:
Given the remainders from dividing an integer n by an arbitrary set of divisors, the remainder when n is divided by the least common multiple of those divisors is uniquely determinable.
If the divisors are pairwise coprime, their LCM is their product, which is slightly easier to compute, which is why the CRT is usually presented in this more restrictive form (less arbitrary). A proof by construction is typical — show how to find the unique solution — and prove the construction correct.
Here's an example of this method using the system Til had Abu and Ila solve:
| N | Congruence form | Equivalent modulus form |
|---|---|---|
| 1. | \(x\ \equiv_7\ 4\) | \(x\ \%\ 7 = 4\) |
| 2. | \(x\ \equiv_{11}\ 2\) | \(x\ \%\ 11 = 2\) |
| 3. | \(x\ \equiv_{13}\ 9\) | \(x\ \%\ 13 = 9\) |
3.3.3 WZC
| 143y1 | ≡7 | 1 | → | y1 | = | -2 |
| 91y2 | ≡11 | 1 | → | y2 | = | 4 |
| 77y3 | ≡13 | 1 | → | y3 | = | -1 |
So x = 4 × 143 × -2 + 2 × 91 × 4 + 9 × 77 × -1
= 4 × -286 + 2 × 364 + 9 × -77
= -1144 + 728 + -693
= -1109
Now add 1001 twice to get 893. Why 1001? Why twice?
Because we want TUMMI, so it must be a number between 0 and 1001 (actually 1000).
This construction works because of the following facts:
| -286 | ≡7 | 1 | ≡11 | 0 | ≡13 | 0 |
| 364 | ≡7 | 0 | ≡11 | 1 | ≡13 | 0 |
| -77 | ≡7 | 0 | ≡11 | 0 | ≡13 | 1 |
If you've studied any linear algebra, and have solved a system of simultaneous equations using a method like Gaussian Elimination, the 0-1 matrix embedded above should ring a bell.
3.3.4 FIL
There are two main applications of the CRT — computer arithmetic with large numbers, and the RSA Cryptosystem. Both are topics worth exploring.
4 THR
"We've been drawing trees left to right, but let's switch to the more traditional top to bottom view," said Til. Abu smiled. "I remember reading in that book of his you had us read, Pinker said something about how 'botanically improbable' growing trees from the root down is!"
"Improbable or not, let's grow some trees," Til continued. "Build them from scratch. Construct them from cells. Not actual biological cells, that would take too long – we'll use memory cells. Storage cells in computer memory take many forms, but in lisp, a cell looks like this"
[car|cdr]
"More TLAs?" said Ila. "Yes," replied Til, "but you're going to have to find out what they mean on your own."
Not too reluctantly nodding her assent, Ila saw flashes of race cars and compact disk readers as Til went on. "The car and the cdr (pronounced could-er) go hand in hand in a memory companionship. Think of this construct (abbreviated cons) as a dyad — a structure of two things. Actually, these two things are pointers to two other things. The things on either side can be atoms or non-atoms (molecules)."
"So an atom is like a number or a symbol, and a molecule is like a list or a vector?" Abu said. "Yes, or like a string?" Ila jumped in. "Mostly yes to you, Abu; but no to you, Ila," said Til. "A string is an atom too?" Ila sighed. Til nodded. "Is there a predicate to tell the difference?" said Abu. "Indeed!" said Til. "What do you suppose its name is?!"
-~-~-~-~-~-
4.1 STU
Cars and cdrs. Abbreviated, the car is a forward slash (pointing down to the left) and the cdr is a backward slash (pointing down to the right). Then a cons cell without 'pointees' looks like:
[/|\]
And with pointees:
[/|\] a b
In lisp-speak this is a dotted pair, so named because its printed representation separates car from cdr by a dot (period):
(cons 'a 'b) evaluates to (a . b)
A list is built with a chain of cons cells:
(cons 'a (cons 'b (cons 'c (cons 'd nil)))) evaluates to (a b c d)
[/|-]-->[/|-]-->[/|-]-->[/|_] a b c d
A tree is built differently:
(cons (cons 'a 'b) (cons 'c 'd)) ; evaluates to ((a . b) c . d) [/|\] [/|\|/|\] a b c d
(cons
(cons
(cons 'a 'b)
(cons 'c 'd)
)
(cons
(cons 'e 'f)
(cons 'g 'h)
)
) ; evaluates to: (((a . b) c . d) (e . f) g . h)
[/|\]
/ \
[/|\] [/|\]
/ \ / \
[/|\][/|\][/|\][/|\]
a b c d e f g h
Now we know how trees look as cons cells consed together, we can render them without the clutter of the containers:
/\
a b
/\
/ \
/\ /\
a b c d
/\
/ \
/ \
/ \
/\ /\
/ \ / \
/\ /\ /\ /\
a b c d e f g h
/\
/ \
/ \
/ \
/ \
/ \
/ \
/ \
/\ /\
/ \ / \
/ \ / \
/ \ / \
/\ /\ /\ /\
/ \ / \ / \ / \
/\ /\ /\ /\ /\ /\ /\ /\
a b c d e f g h i j k l m n o p
These growth patterns can continue to any depth, but this is enough for now. Before proceeding, let's lay out the common nomenclature for things knobby and smooth. (Lots of VTOs ahead, so we'll dispense with that marker.)
A node is the knobby thing (drawn as a two-dimensional circle or box), also called a vertex (plural vertices).
A link is the smooth thing (drawn as a one-dimensional line), also called an edge.
A tree is a collection of nodes and links, the links connecting nodes to other nodes such that there is only one path from one node to any other node. If there is more than one path, it's not a tree, it's a graph. More on which later.
A path is a sequence of links from node to node. A proper link
sequence has shared nodes between successive links. Think of a link
as an ordered pair (like a cons) of nodes. So to be a sequence, the
first node of a link must be the second node of its preceding link;
likewise, the second node of a link must be the first node of its
following link. Writing nodes as letters and links as pairs of
letters (TWO-letter-acronyms), ab bc cd is a valid sequence, but
ab cb cd is not.
A tree always has one more node than it has links. Always. Visualize starting with a seedling that has only one node (sometimes called a degenerate tree). This singleton node has zero links. One is one more than zero.
Let's render a node as a star:
*
Adding one link also adds a node at the other end. Now there are two nodes and one link.
* / *
Add another link (with its other-end node) to the first node and now there are three nodes and two links:
* / \ * *
In lisp:
(cons (cons nil nil) (cons nil nil)) ; ((nil) nil)
Or
(cons (cons t t) (cons t t)) ; ((t . t) t . t)
It seems like an obvious pattern: one cons cell for every node (star). One cons call takes two arguments. Two (arguments) is one more than one (cons call). So counting total calls and arguments, there's always one more argument (nodes) than there are calls (links).
But that's wrong! The correct way to count nodes and links is as follows:
A cons call creates a node for itself, a link for its first
argument and another link for its second argument. But two links
for one node is the reverse of what it should be. The trick is to
only count arguments as links if they are NON-nil. A nil argument
is like a null pointer. So (cons nil nil) is the singleton node
with no links. A cons call also creates a node for each NON-cons
argument. The consp predicate tells whether or not the lisp
object given it is a cons cell.
(consp OBJECT) ; Returns t if OBJECT is a cons cell.
| Expression | Evaluates To |
|---|---|
(consp t) |
nil |
(consp nil) |
nil |
(consp SYMBOL) |
nil |
(consp NUMBER) |
nil |
(consp (cons 'a 'b)) |
t |
The expression (cons 'a 'b) creates the three-node two-link tree:
* / \ a b
A binary tree (the kind depicted so far) has two links emanating from each node. Factor trees are binary, e.g.:
1234 5678
/\ /\
2 617 2 2839
/\
17 167
To generalize, an m-ary tree has nodes with m links, or rather up to m links, but to be a regular tree, all its nodes must have exactly m. Returning to a counting theme, a connection between Elementary Generative Combinatorics (EGC) and trees was alluded to earlier. Generating lists of combinations of things allows counting these combinations by simply getting the length of a list. Factor trees generate prime factors, with easy-to-count leaves, but a different m (also called branching factor) in different parts of the tree applies to generating all factors. The 24 factors of 360, whose prime factorization is \(2^3 \cdot 3^2 \cdot 5\), are here listed at the bottom of this tree:
Start the branching with 4 powers of 2: /\
_//\\_
______2^0=1_______/ / \ \________2^3=8______
/ / \ \
___________/ 2^1=2__/ \__2^2=4_ \___________
/|\ /|\ /|\ /|\
/ | \ / | \ / | \ / | \
Multiply everything on the level just above by 3 powers of three: 3^0, 3^1 and 3^2| \
/ | \ / | \ / | \ / | \
1 3 9 2 6 18 4 12 36 8 24 72
/ | \ / | \ / | \ / | \
Multiply everything here by 2 powers of five: 5^0 and 5^1 | \ / | \
/ | \ / | \ / | \ / | \
/ \ / \ / \ / \ / \ / \ / \ / \ / \ / \ / \ / \
/ \ / \ / \ / \ / \ / \ / \ / \ / \ / \ / \ / \
1 5 3 15 9 45 2 10 6 30 18 90 4 20 12 60 36 180 8 40 24 120 72 360
Multiplying together the three branching factors, 4 * 3 * 2 = 24, gives the total leaf count.
Another m-ary tree example is a permutation tree. For instance, to
generate all 24 (\(4! = 4 \times 3 \times 2 \times 1\)) permutations
of [1 2 3 4], m goes from 4 to 3 to 2 to 1 as the tree grows:
1234
/\
/||\
_________________/ /\ \________________
/ / \ \
1 / ____2______/ \_____3___ \ 4
/ / \ \
/ / \ \
________________/ | | \________________
/ | | \
2 3 4 1 3 4 1 2 4 1 2 3
/ | \ / | \ / | \ / | \
/ | \ / | \ / | \ / | \
/ | \ / | \ / | \ / | \
/ | \ / | \ / | \ / | \
/ | \ / | \ / | \ / | \
/ | \ / | \ / | \ / | \
/ | \ / | \ / | \ / | \
34 24 23 34 14 13 24 14 12 23 13 12
/ \ / \ / \ / \ / \ / \ / \ / \ / \ / \ / \ / \
4 3 4 2 3 2 4 3 4 1 3 1 4 2 4 1 2 1 3 2 3 1 2 1
| | | | | | | | | | | | | | | | | | | | | | | |
1234 1243 1324 1342 1423 1432 2134 2143 2314 2341 2413 2431 3124 3142 3214 3241 3412 3421 4123 4132 4213 4231 4312 4321
In a binary tree a node is also allowed to have only one link; if so, we say it lacks 'completeness' or 'fullness'. Some nodes legitimately have zero links. These are the leaf nodes, or the leaves of the tree. Mixing the botanical and the genealogical metaphors, a leaf node is also called a childless node. The children of non-leaf nodes are distinguishable as either the left child or the right child.
The node whose children are u and v is naturally called the
parent of u and v. That makes u and v siblings in this
family tree. The parent of the parent of u is its grandparent,
u is its grandparent's grandchild, and so on, with ancestor
and descendant likewise defined genealogically.
Rooted trees differ from unrooted (or free) trees by having a single node designated as the root. Family tree relationships hold only in rooted trees, which breaks the symmetry of "is-related-to" (a node is related to another node by a link connecting them) into a child-to-parent or parent-to-child direction. Downwards away from the root goes parent-to-child, upwards towards the root goes child-to-parent. The level of a node is the number of links between it and the root. The root node has level 0. The maximum level taken over all leaf nodes is the height (or depth) of the tree.
Back to building, creating the tree
/\ a /\ b c
in lisp is easy, it's (cons 'a (cons 'b 'c)), with 5 nodes and 4
links. The level of leaf node a is 1, the level of both b and c
is 2, so the height of the tree is (max 1 2 2) = 2.
Now we'll build this tree:
/\
a \
/\
b \
/\
c \
/\
d nil
From the bottom up, start with (cons 'd nil). Moving up a level,
wrap that cons in another cons with car 'c: (cons 'c (cons 'd
nil)). Continuing up the levels, (cons 'a (cons 'b (cons 'c (cons 'd
nil)))). In other words, this tree is really the list (a b c d),
with 9 nodes and 8 links, and its height is the length of the list,
namely 4.
| Node | Level |
| a | 1 |
| b | 2 |
| c | 3 |
| d | 4 |
In these simple examples, internal (non-leaf) nodes are different than leaf nodes, in that the latter are the only ones whose car and cdr pointees can be actual (non-cons) data. So building trees that store arbitrary data items at all nodes, in addition to left- and right-child links, requires a different tactic, a GPAO.
4.1.1 ORU
Applications
We now turn our attention to two tree applications whose beauty and utility give them superstar status:
- fast searching
- data compression
In searching for an item in a list of orderable items, there is a slow (less efficient) way and a fast (more efficient) way. The less efficient way is linear search — or sequential search — in which the searched-for item (called a key) is compared with each item in the list (or array/vector — indeed any sequence type) in a linear left-to-right front-to-back order. The items in the list can be in any order, but orderable items are ones that can be sorted. First putting them in sort order (typically, ascending — from "smallest" to "largest") leads to the more efficient way, called binary search. The non-tree binary search algorithm normally uses an indexable array of data. We'll skip taking a closer look at that and just focus on the tree version.
Key comparisons are usually three-way, but it takes a nested if
to discern:
- key1 < key2
- key1 = key2
- key1 > key2
as in the following example, which illustrates orderable numbers as keys:
(let ((items (list 1 2 3 4)) (key 3)) (loop for item in items collect (if (< key item) "<" (if (= key item) "=" ">")))) ; evaluates to: (">" ">" "=" "<")
The same code in more functional style:
(let ((items (list 1 2 3 4)) (key 3)) (mapcar (lambda (item) (if (< key item) "<" (if (= key item) "=" ">"))) items)) ; also evaluates to: (">" ">" "=" "<")
In binary search, after each step the search time is cut in half, so a list of size 16 is reduced to a list of size 1 in 4 steps (counting arrows in \(16 \rightarrow 8 \rightarrow 4 \rightarrow 2 \rightarrow 1\)). A size-one list is easy to search, just check whether or not its single element compares as equal to the search key.
A binary search tree (BST) is a binary tree with a key at each node such that all keys in the node's left descendants (i.e., subtree) are less than the node's key, and all keys in the node's right descendants (i.e., subtree) are greater than the node's key. And of course, all keys at the node itself (all one of them) are equal to that one key. Note that this application of trees requires 'beefier' nodes than cons cells can easily provide.
Other characteristics of BSTs, where n is the number of nodes (keys), and h is the height of the tree, include:
- Search time is a logarithmic function of n (assuming a balanced tree — see below).
- Insertion of a key is equally fast: search for the key, insert it at the leaf where the search terminates.
- For all operations (search, insert, delete) the worst case number of key comparisons = h + 1.
- \(\lfloor \mbox{lg}\ n\rfloor \le h \le n - 1\)
- With average (random) data: \(h < 1.44\ \mbox{lg}\ n\)
- With a poorly built (unbalanced) tree, in the worst case binary search degenerates to a sequential search.
- Inorder traversal produces a sorted list (the basis for the treesort algorithm).
Building a BST
To build a binary search tree for a set of words, use alphabetical order for ordering the keys/words, as in:
[trees are cool and the binary search kind wonderfully so]
Step 1, insert 'trees as the root of the BST
trees
Step 2, insert 'are as the left child of 'trees since 'are < 'trees
trees
/
are
Step 3, insert 'cool as the right child of 'are since 'cool < 'trees and 'cool > 'are
trees
/
are
\
cool
Step 4, insert 'and as the left child of 'are since 'and < 'trees and 'and < 'are
trees
/
are
/ \
and cool
Step 5, insert 'the as the right child of 'cool since 'the < 'trees and 'the > 'are and 'the > 'cool
trees
/
are
/ \
and cool
\
the
Step 6, insert 'binary as the left child of 'cool since 'binary < 'trees and 'binary > 'are and 'binary < 'cool
trees
/
are
/ \
and cool
/ \
binary the
Step 7, insert 'search as the left child of 'the since 'search < 'trees and 'search > 'cool and 'search < 'the
trees
/
are
/ \
and cool
/ \
binary the
/
search
Step 8, insert 'kind as the left child of 'search since that's where it goes
trees
/
are
/ \
and cool
/ \
binary the
/
search
/
kind
Step 9, insert 'wonderfully where it goes (finally a right child for root!)
trees
/ \
are wonderfully
/ \
and cool
/ \
binary the
/
search
/
kind
Step 10, insert 'so where it goes, and the tree is complete.
trees
/ \
are wonderfully
/ \
and cool
/ \
binary the
/
search
/ \
kind so
4.1.2 XAD
Post-construction Binary Search Tree Insertion
To insert a new word, very, into this BST, we must compare it to 'trees, then 'wonderfully. At this point the search terminates, because 'wonderfully has no children. Note we needed two comparisons to find 'very's insertion site, as the left child of 'wonderfully. If a key is already in the BST, insertion of that key has no effect. It still costs some comparisons, however. Inserting (futilely) 'cool costs 3 comparisons (the level of 'cool plus one), and 'kind costs 6 comparisons.
4.1.3 GJM
Expected Search Cost
Binary search trees have expected search costs, which simply put is the average cost of finding a key. Minimizing this cost for a static (unchanging) tree and a set of keys whose access frequencies are known in advance (think English words as might be used by a spell-checker) is the Optimal BST scenario. GPAO.
Keys' search costs can be weighted based on how likely they are to be looked up. Estimates of these likelihoods are usually good enough if they can't be computed exactly, and the more accurate the estimates, the speedier the average lookup. So an optimal BST would have a common word like is near the root and a rarely used word like syzygy near the leaves. Here are the search costs (number of key comparisons) for the tree above:
UnBalanced
| Key | Cost |
|---|---|
| and | 3 |
| are | 2 |
| binary | 4 |
| cool | 3 |
| kind | 6 |
| search | 5 |
| so | 6 |
| the | 4 |
| trees | 1 |
| wonderfully | 2 |
| Total | 36 |
Average cost: 3.6 comparisons
Balanced
| Key | Cost |
|---|---|
| and | 3 |
| are | 2 |
| binary | 3 |
| cool | 1 |
| kind | 4 |
| search | 3 |
| so | 4 |
| the | 2 |
| trees | 3 |
| wonderfully | 4 |
| Total | 29 |
Average cost: 2.9 comparisons
A Huffman tree is like an optimal BST, but with a twist. It has a
different goal, that of encoding information efficiently, meaning it
minimizes the average number of bits per symbol (information atom). A
Huffman tree does this by storing more frequently-seen symbols closer
to the root and less-frequently-seen symbols further from the
root. Bits (1s and 0s) are used to label the links on the path
from root to leaf, giving a unique bit string encoding for each
symbol.
Unlike a BST, a Huffman tree does not care about key order, and it doesn't use internal (non-leaf) nodes to store the data (neither keys nor bits). The only data items are the symbols, stored at the leaves. The symbols' encodings are stored in the structure of the tree. For example, consider the symbols A through F with the given frequencies:
| symbol | A | B | C | D | E | F |
| frequency | 0.08 | 0.10 | 0.12 | 0.15 | 0.20 | 0.35 |
The encoding process begins with an initial forest of trees (seedlings, actually). These are conveniently stored in a priority-queue — a data structure where high-priority items are always maintained at the front of the queue. The nodes in this collection are ordered by lowest-to-highest frequencies, as in the table above, shown paired below.
([A 0.08] [B 0.10] [C 0.12] [D 0.15] [E 0.20] [F 0.35])
The algorithm for building a Huffman tree creates an initial queue Q of 1-node trees from pairs of n symbols and n weights, which can be passed as pairs or as parallel arrays. The weights are the frequencies — how often the symbols (e.g., characters) occur in some information (e.g., a body of text). These weights/frequencies define the priorities of the symbols, reverse ordered, so the lower the weight, the higher the priority. Once the tree is built, the weights can be forgotten, all that matters is where the symbols are found in the tree.
Algorithm Huffman Tree (inputs and initialization of Q as above) while Q has more than one element do TL ← the minimum-weight tree in Q Delete the minimum-weight tree in Q TR ← the minimum-weight tree in Q Delete the minimum-weight tree in Q Create a new tree T with TL and TR as its left and right subtrees, and weight equal to the sum of TL's weight and TR's weight. Insert T into Q. return T
Here's how the algorithm proceeds with the given example, using the phrase consolidate u and v into a parent node (with weight w) inserted after x as an abbreviation for the steps in the body of the loop:
Q: [A 0.08] [B 0.10] [C 0.12] [D 0.15] [E 0.20] [F 0.35]
Iteration 1, consolidate [A 0.08] and [B 0.10] into a parent node (with weight 0.18) inserted after D:
Q: [C 0.12] [D 0.15] [+ 0.18] [E 0.20] [F 0.35]
/ \
[A 0.08] [B 0.10]
Iteration 2, consolidate [C 0.12] and [D 0.15] into a parent node (with weight 0.27) inserted after E:
Q: [+ 0.18] [E 0.20] [+ 0.27] [F 0.35]
/ \ / \
[A 0.08] [B 0.10] [C 0.12] [D 0.15]
Iteration 3, consolidate [+ 0.18] and [E 0.20] into a parent node (with weight 0.38) inserted after F:
Q: [+ 0.27] [F 0.35] [+ 0.38]
/ \ / \
[C 0.12] [D 0.15] [+ 0.18] [E 0.20]
/ \
[A 0.08] [B 0.10]
Iteration 4, consolidate [+ 0.27] and [F 0.35] into a parent node (with weight 0.62) inserted after [+ 0.38]:
Q: [+ 0.38] [+ 0.62]
/ \ / \
[+ 0.18] [E 0.20] [+ 0.27] [F 0.35]
/ \ / \
[A 0.08] [B 0.10] [C 0.12] [D 0.15]
Iteration 5, consolidate [+ 0.38] and [+ 0.62] into a parent node (with weight 1.00) inserted back into Q:
Q: [+ 1.00]
/ \
/ \
/ \
[+ 0.38] [+ 0.62]
/ \ / \
[+ 0.18] [E 0.20] [+ 0.27] [F 0.35]
/ \ / \
[A 0.08] [B 0.10] [C 0.12] [D 0.15]
Q no longer has more than one element, so exit the while loop and return the tree T ([+ 1.00]).
What the embedded encoding is will become clear, but here's a preview:
| A | 000 |
| B | 001 |
| C | 100 |
| D | 101 |
| E | 01 |
| F | 11 |
By virtue of its construction as a tree, this encoding is prefix-free, meaning no symbol's bit string is a prefix (initial substring) of any other symbol's bit string. The compression is not great, but serves to illustrate the point of all this work. A quick measure of this encoding's success is, what is the average number of bits used to encode a character?
\(3 \cdot 0.08 + 3 \cdot 0.10 + 3 \cdot 0.12 + 3 \cdot 0.15 + 2 \cdot 0.20 + 2 \cdot 0.35 = 2.45\)
4.1.4 PSV
Huffman Encoding
- Traverse the binary tree and generate a bit string for each node of the tree as follows:
- Start with the empty bit string for the root;
- append 0 to the node's string when visiting the node's left subtree begins;
- append 1 to the node's string when visiting the node's right subtree begins.
- At a leaf, print out the current bit string as the leaf's encoding.
A Huffman tree with n leaves has a total of 2n - 1 nodes, each of which must be visited to generate the leaf nodes' strings. But since each node has a constant height, the efficiency of this algorithm is very good — linear in the number of nodes.
Given this code:
| A | 000 |
| B | 001 |
| C | 100 |
| D | 101 |
| E | 01 |
| F | 11 |
the text CAFEBABE is encoded as 100000110100100000101, a total of
21 bits. (This beats the fixed-length encoding scheme [A=000 B=001
C=010 D=011 E=100 F=101] that requires 3 bits per character and a
total of 24 bits 010000101100001000001100 for the 8-character string.)
4.1.5 YBE
Huffman Decoding
A bit string (e.g., 0010001011100010101) is decoded by considering
each bit from left to right, and starting at the root, traversing left
if the bit is 0 and traversing right if the bit is 1, stopping when a
leaf is reached. Output the symbol at the leaf, and continue with the
next bit.
| 001 | 000 | 101 | 11 | 000 | 101 | 01 |
| B | A | D | F | A | D | E |
4.2 VWX
"What are potential applications of graphs?" said Til. "Anything and everything!" he answered his own question. And went on. "You know the general meaning of the term 'graphs' in everyday math — a plot or chart of numerical data using a coordinate system — as in graphs of functions. Well, from now on when you hear the term I want you to think first of its special meaning in discrete mathematics, where a graph is a technical type of discrete structure that is useful for representing relations."
"Graphs can represent relations, and relations can describe the extension of any predicate, so anything describable by relations is representable by graphs," Til said, and paused, and right in tempo Ila asked, "What does that mean, a predicate's extension?" "I think I know," Abu said. "It's the set of all true facts that predicate describes. But can't that set be infinite? How does a graph represent that?" "Very carefully," Til chuckled and winked.
-~-~-~-~-~-
Some applications of graphs:
- Networking
- Scheduling
- Flow optimization
- Circuit design
- Path planning
- Genealogy analysis
- Computer game-playing
- Program compilation
- Object-oriented design (think UML)
And the list goes on and on …
Others for GPAO:
- Acquaintanceship Graphs
- Influence Graphs
- The Hollywood Graph
- Collaboration Graphs
- Round-Robin Tournament Graphs
- Call Graphs
- Etc., Etc., Etc.
Graphs have this intuitive knobs-and-lines visual representation, just like trees. The difference is, of course, that graphs allow cycles, a path from a node back to itself, which also implies the existence of more than one path from one node to another (ponder that). In this way graphs generalize trees analogous to the way relations generalize functions.
4.2.1 HKN
Simple Graphs
- Correspond to symmetric binary relations.
- Have V, a set of Vertices or Nodes (corresponding to the universe of some relation R).
- Have E, a set of Edges or Arcs or Links (unordered pairs of usually distinct, possibly the same elements \(u, v \in V\) such that uRv).
- Are compactly described as a pair G = (V, E) (with R implied).
Here's an example of a simple graph having V, the set of states in the Intermountain West:
- V =
[ID MT WY UT CO NV AZ NM] - E = \(\{[u\ v] \mid u\ \mbox{adjoins}\ v\} =\) =([ID MT] [ID WY] [ID NV] [ID UT] [MT WY] [WY UT] [WY CO] [UT CO] [UT NV] [UT AZ] [CO NM] [AZ NM] [NV AZ])=
Multigraphs
- Are like simple graphs, but there may be more than one edge connecting two given nodes.
- Have V, a set of Vertices.
- Have E, a set of Edges (as primitive objects).
- Have f, a function \(f : E \rightarrow \{(u,v) \mid u,v \in V \land u \ne v\}\)
- Are compactly described as a triple: G = (V, E, f)
For example, vertices are cities, edges are segments of major highways.
Pseudographs
- Are like multigraphs, but edges connecting a node to itself are allowed.
- The function \(f : E \rightarrow \{(u,v) \mid u,v \in V\}\)
- Edge \(e \in E\) is a loop if \(f(e) = (u, u) = \{u\}\)
Directed Graphs
- Correspond to arbitrary binary relations R, which need not be symmetric.
- Have V, E, and a binary relation R on V.
For example, V = people, \(R = \{(x, y) \mid x\ \mbox{loves}\ y\}\)
Directed Multigraphs
- Like directed graphs, but there may be more than one edge from one node to another.
- Have V, E, and \(f : E \rightarrow V \times V\).
4.2.2 QTW
TGB: Terminology Gone Ballistic.
Adjacent, Connects, Endpoints, Initial, Terminal, Degree, In-degree, Out-degree, Complete Graphs, Cycles, Wheels, n-Cubes, Bipartite Graphs, Subgraph, Union, …
Adjacency
Let G be an undirected graph with edge set E. Let \(e \in E\)
be (or map to) the pair [u v].
We say:
- u and v are adjacent
- u and v are neighbors
- u and v are connected
- Edge e is incident with nodes u and v
- Edge e connects u and v
- Nodes u and v are the endpoints of edge e
Degree
Let G be an undirected graph, \(v \in V\) a vertex.
- The degree of v, denoted deg(v), is the number of incident edges to it, except that any self-loops are counted twice
- A vertex with degree 0 is called isolated
- A vertex with degree 1 is called pendant
Degree Sequence
A sequence of the degrees of all nodes in a graph, listed in nonincreasing order (highest to lowest), is the graph's degree sequence.
For example, the degree sequence of the knobs-and-lines graph is:
[5 5 4 4 4 4 4 3 3 2]
Handshaking Theorem
Let G be an undirected (simple, multi-, or pseudo-) graph with vertex set V and edge set E. Then the sum of the degrees of the vertices in V is twice the size of E:
\[\sum_{v \in V} deg(v) = 2|E|.\]
Directed Adjacency
Let G be a directed (possibly multi-) graph and let e be an
edge of G that is (or maps to) [u v].
- u is adjacent to v
- v is adjacent from u
- e comes from u
- e goes to v
- e connects u to v
- e goes from u to v
- u is the initial vertex of e
- v is the terminal vertex of e
Directed Degree
Let G be a directed graph, v a vertex of G.
- The in-degree of v, \(deg^-(v)\), is the number of edges going to v
- The out-degree of v, \(deg^+(v)\), is the number of edges coming from v
- The degree of v is just the sum of v's in-degree and out-degree, \(deg(v) = deg^-(v) + deg^+(v)\)
Directed Handshaking Theorem
Let G be a directed (possibly multi-) graph with vertex set V and edge set E. Then
\[\sum_{v \in V} deg^-(v) = \sum_{v \in V} deg^+(v) = \frac{1}{2} \sum_{v \in V} deg(v) = |E|.\]
Note that the degree of a node is unchanged by whether its edges are directed or undirected.
Special Graph Structures
Special types of undirected graphs:
- Complete graphs Kn
- Cycles Cn
- Wheels Wn
- n-Cubes Qn
- Bipartite Graphs
- Complete bipartite graphs \(K_{m, n}\)
Complete Graphs
For any \(n \in N\), a complete graph on n nodes (Kn) is a simple graph with n nodes in which every node is adjacent to every other node.
- \(\forall u, v \in V : u \ne v \rightarrow (u, v) \in E\).
Note that Kn has n-choose-2 for its number of edges:
\[\sum_{i = 0}^{n - 1}i = \frac{n(n - 1)}{2}.\]
Cycles
For any \(n \ge 3\), a cycle on n nodes (Cn) is a simple graph where
- \(V = \{v_1, v_2, \ldots, v_n\}\) and
- \(E = \{(v_1, v_2), (v_2, v_3), \ldots, (v_{n - 1}, v_n), (v_n, v_1)\}\).
Wheels
For any \(n \ge 3\), a wheel (Wn) is a simple graph obtained by taking the cycle Cn and adding one extra node \(v_{hub}\) and n extra edges.
- \(\{(v_{hub}, v_1) (v_{hub}, v_2), \ldots, (v_{hub}, v_n)\}\).
n-cubes
For any \(n \in N\), the n-cube (or hypercube) Qn is a simple graph consisting of two copies of \(Q_{n - 1}\) connected together at corresponding nodes.
Subgraph
A subgraph of a graph G = (V, E) is any graph H = (W, F) where \(W \subseteq V\) and \(F \subseteq E\).
Graph Union
The union \(G_1 \cup G_2\) of two simple graphs \(G_1 = (V_1, E_1)\) and \(G_2 = (V_2, E_2)\) is the simple graph \((V_1 \cup V_2, E_1 \cup E_2)\).
4.3 YZ@
CSP more high-level TAI interaction.
4.3.1 ZCF
CSP definitions, examples, VTOs.
4.3.2 ILO
CSP a discussion of the Chomsky Hierarchy.
5 )
Where the Book Ends is a starting point for Further Learning Adventures (FLAs).
- This book is not about that kind of word play
- According to http://www.urbandictionary.com/define.php?term=metaphors%20be%20with%20you, the phrase I'm using for this book's title has been around awhile. I honestly do not know whether I heard or read it online first, or if I thought it up independently. No matter. Come day number four of month number five, all things Star Wars come to mind. ☺
The debate rages on whether the adjective in the subtitle should be tireless or timeless. Perhaps in a future printing the cover will have a hologram showing it both ways, depending on the angle of view.
Perhaps not. Ascribing the timelessness quality to one's own work is the height of hubris. The pinnacle of presumption. The acme of arrogance. The depth of debauchery. The very idea. (Wait, that breaks the pattern. ☺)
So it is tireless — leaving the r-to-m transformation to its own devices. Perhaps in that iffy future holographic printing the transformation (transfiguration?) can be an animation that looks like a natural process, like wax melting under a flame, or gravity dictating the bounce of a ball. In the meantime, it is what it is — an obvious ploy for humor's sake? Or perhaps just a PWCT?
Parallel Word-Chain Transformations chain a sequence of word transformations in lock-step. So maybe the 'a'-less subtitle could move from "tireless work on play on words" to "tineless fork in clay of woods" to "tuneless dork is claw if goods" and from thence (some would say already) into madness and nonsense. ☺
Just say no. See word/phrase/sentence transformations for what they are — discrete mathematical operations on strings and sequences of strings. No deeper meaning to them need be linked.
- rounds out the dyad
- Something consisting of two elements or parts is called a dyad. End of freebies. Upon encountering an unfamiliar word, from now on the reader is encouraged to apply a principle introduced in http://emp.byui.edu/neffr/mymanifesto.html. So what is a monad? A triad? Tetrad? Pentad? What comes next in this progression?
- Isaiah 28:10
- Read this verse at https://www.lds.org/scriptures/ot/isa/28?lang=eng#10 and then map the acronym-expand function to [LUL PUP HAL TAL].
- A quick review and preview
- Thanks to the last responder at https://www.quora.com/How-should-I-go-about-switching-from-an-object-orientated-way-of-thinking-to-a-more-functional-way-of-thinking
- any conceptual (as opposed to botanical) tree
- The reader is presumably familiar with hierarchical organization charts, family trees, tournament trees, perhaps even decision trees, to name a few.
- PSG ISA TLA TBE l8r
- To elabor8, TBA and TBD and TBE and TBR and the like are just TLAs interpreted by concatenating Arranged and Determined and Examined and Revealed and et cetera to To Be.
- diphthongs
- How laaaa-eekly is it that a random reader knows what these are?
- Not every language's alphabet is so easy
- But the Hawaiian alphabet is even easier (smaller at least) — half less one, letters number but twelve: (A, E, H, I, K, L, M, N, O, P, U, and W). Aloha. Mahalo.
- alphabet
- What can happen when an Internet company uses a new Internet TLD (Top-Level Domain) name with three letters to accompany a three-letter host name: https://abc.xyz/
- PENTY, a carefully chosen way to code-say Christmas
PLENTYminus theL— better asABCDEFGHIJKMNOPQRSTUVWXYZas the ultimate in NoelsilLliness. ☺
- IYI
- If You're Interested. I picked up this particular TLA by reading David Foster Wallace's Everything and More: A Compact History of Infinity. HRR, BTW.
- is my high hope
- My maybe-not-quite-so-high hope is that you will enjoy reading this book as much as I have enjoyed writing it. I've done my best to conquer my bad habit of overcomplificationaryizing everything. ☺
- He awoke with a start
- This character is my surrogate. Pedagogically speaking, my using his voice is a choice of a nice device. A sleek technique. A slick trick. A cool tool. A … … (Here we go again.)
- EDGE
- Elphaba Defying Gravity Emphatically, for example. (Note the FLA. Four-Letter Acronym. Which ISN'T. Ambiguous, too. Could mean Five-Letter Acronym.)
- he had acquired years ago
- If you take the time to enjoy it, http://www.amazon.com/Falling-Up-Shel-Silverstein/dp/0060248025 is a sweet treat. And wouldn't you know it, on page 42 is a poem that uses lisp.
- DINK
- Dual Income No Kids
- SINKNEM
- Single Income No Kids Not Even Married
- STEM
- Science Technology Engineering Mathematics
- appreciate the flowers more or less?
- http://www.goodreads.com/quotes/184384-i-have-a-friend-who-s-an-artist-and-has-sometimes
- ABC
- Always Begin Carefully — https://en.wikipedia.org/wiki/ABC
- AKA
- Also Known As — but you already knew that, NEH?
- VTO
- Vocabulary Time Out. There will be many of these.
- the mathematical idea of a set
- A mathematician/computer scientist wrote the following intriguing words: It is impossible to improve upon [Georg] Cantor's succinct 1883 definition: A set is a Many which allows itself to be thought of as a One. One of the most basic human faculties is the perception of sets. […] When you think about your associates and acquaintances you tend to organize your thought by sorting these people into overlapping sets: friends, women, scientists, drinkers, gardeners, sports fans, parents, etc. Or the books that you own, the recipes that you know, the clothes you have — all of these bewildering data sets are organized, at the most primitive level, by the simple and automatic process of set formation, of picking out certain multiplicities that allow themselves to be thought of as unities. Do sets exist even if no one thinks of them? The numbers 2, 47, 48, 333, 400, and 1981 have no obvious property in common, yet it is clearly possible to think of these numbers all at once, as I am now doing. But must someone actually think of a set for it to exist? […] The basic simplifying assumption of Cantorian set theory is that sets are there already, regardless of whether anyone does or could notice them. A set is not so much a "Many which allows itself to be thought of as a One" as it is a "Many which allows itself to be thought of as a One, if someone with a large enough mind cared to try." For the set theorist, the bust of Venus is already present in every block of marble. And a set M consisting of ten billion random natural numbers exists even though no human can ever see M all at once. A set is the form of a possible thought, where "possible" is taken in the broadest possible sense. — Rudy Rucker in Infinity and The Mind: The Science and Philosophy of the Infinite
- dispensing with commas
- IMO, commas are the ugly ducklings in the world of programming language syntax.
- we truncated the set N
- The set N of natural numbers (including zero) is AKA the nonnegative numbers. Clarification: in this context numbers mean integers, numbers with no fractional parts, not even decimal points followed by nothing (or nothing but zeros). The set P is not the set of positive integers, that's called Z+. P names the prime numbers (but not always). Z- is the negative integers, but there's no abbreviation for the nonpositive integers, which is Z- together with 0. All together, Z is the short name for all integers, positive, negative, and zero. Z is short for Zahlen, which is the German word for numbers. Now you know.
- our rule also prefers
- The vectors-over-lists preference has a special reason, revealed IYI. But it's not just its indexability. A lisp list can also be indexed, but the operation is more expensive than a vector index (a quick add offset and pointer dereference), as it must walk the list, counting as it goes. Before we delve here into a bit of algorithm analysis, what is an algorithm? The recipe analogy is often used, but recipes for cooking are not the only kind. For another, far more weighty example, see https://www.lds.org/general-conference/2008/04/the-gospel-of-jesus-christ?lang=eng — but it's interesting that Elder Perry ties the gospel recipe back to the cooking kind. This kind features an implicit "Step 0" that could be made explicit as: "Acquire all required ingredients in the proper quantities." The "List of Ingredients" is usually the first component of a recipe, with "Directions" second.
- handing it off to some further processing step
- How the emacs
elisp Read-Evaluate-Print Loop (
REPL) works is discovered via GPA.
- Boolean values
- George Boole is who this data type is named for, mostly because of his seminal book shortnamed the The Laws of Thought. (What is its longer name?)
- just use true and false
- These global variables must be defined
before you try to use them. Putting, e.g.,
(require 'ment)at the top of your.elsource code file will work provided you have supplied a package namedmentto your emacs lisp environMENT. A package in lisp is a module (library, body of code) that is defined in a global namespace. The package name is a symbol (making it unique) and the named package is found and loaded on two conditions: one, it is in a file named <package-name>.el[c] that has the form(provide '<package-name>)in it (typically as the last line of the file), and two, the file is somewhere in the load path (in emacs,load-pathis an elisp global variable, but other lisps have something equivalent). When does a package get loaded? The(require '<package-name>)special form sees to it. (The single quote preceding <package-name> suppresses evaluation of the <package-name> symbol.)
- kind of wishy-washiness
- I used to think I was indecisive, but now I'm not so sure. ☺
- the 'exclusive' or
- Contrasted with the 'inclusive' or — "p or q" is true if either p is true or q is true, OR BOTH. For 'exclusive' or, replace "OR BOTH" with "BUT NOT BOTH".
- simpler versions of itself
- There's a different kind of
recursive flavor to this never-ending "dialogue" that leads to
less and less simple versions of itself:
- Sue: I'm happy.
- Tom: I'm happy you're happy.
- Sue: I'm happy you're happy I'm happy.
- Tom: I'm happy you're happy I'm happy you're happy.
- …
- eight possibilities
- This is because eight equals two to the
third power. Just like two choices (21) expand to four (22)
when for each of two choices we must make another binary
choice. Thence to 8, 16, 32, … or 2n where
nis the number of true-or-false yes-or-no in-or-out on-or-off … choices made.
- it enables certain useful encodings
- The arithmetization of
logic is used to operationalize logic, and make it more like
doing arithmetic. For example,
not(as innot 1 = 0, not 0 = 1) becomes the subtraction-from-one operation. Compound propositional formulas can be encoded in useful ways as well. One useful encoding turns a Boolean formula φ into a polynomial equation E in many variables. This clever encoding is such that φ is satisfied if and only if E has integral roots.
- Make it so.
- Captain Picard really started something here: https://www.youtube.com/watch?v=RrG4JnrN5GA
- much more than that
- A nice metaphor for a symbol is found here: https://www.gnu.org/software/emacs/manual/html_node/eintr/Symbols-as-Chest.html#index-Chest-of-Drawers_002c-metaphor-for-a-symbol (which is not a bad introduction to programming in elisp: https://www.gnu.org/software/emacs/manual/html_node/eintr/index.html#SEC_Contents).
- If you try it, an error results
When the elisp debugger's ∗Backtrace∗ buffer pops up with the following information:
Debugger entered–Lisp error: <a lispy description of the error>
<a stack trace showing the error's code path>
you should probably just quit, and not worry just yet about learning the intricate ins and outs of elisp debugging. The
Qkey is your friend.
- numbers self-evaluate
- Kind of like TLA self-describes. What other data types do you think self-evaluate in lisp?
- DEF
- Do Everything First — https://en.wikipedia.org/wiki/DEF
- xkcd comic that compares lisp
- http://www.explainxkcd.com/wiki/index.php/297:_Lisp_Cycles. The really deep dive into lisp lore is found at http://www.buildyourownlisp.com/ — but it's not for the faint of heart.
- With your pads
- Or rather, PADS — Personal Assistive Device Stylus — imagine the possibilities …
- any restrictions on what objects
- Not in lisp. This powerful language allows even functions themselves to be inputs and outputs to/from other functions.
- non-trivial task
- Made more so by lisp's dynamic (as opposed to static) typing, which means variables don't have declared types, they can store any type during their lifetime.
- they have a special name
- When talking about logic, the noun
predicate — to quote from the dictionary — "is that part
of a proposition that is affirmed or denied about the subject."
For example, in the proposition "We are mortal," "mortal" (or
"is-mortal" or "are-mortal") is the predicate. Any statement
about something could "predicate" (the verb form) some general
term of that thing; however, convolution may result. For
example, "The main purpose of the Doctrine and Covenants […]
is to implement the law of consecration." It's not easy to pull
out a term which, predicated of "the Doctrine and Covenants",
has the same meaning. So if we're saying
P(x), wherexstands for "the Doctrine and Covenants", what doesPstand for? How about this?Pstands for "to-implement-the-law-of-consecration-main-purpose-of". Just sayingP(x)(or lisp-style,(P x)) is easier. Let it stand for any desired sentence with anxin it. It's not necessary (nor even desirable in most cases) to say whatPstands for by itself.
- how mathematicians think
- See the fascinating book by William Byers at http://www.amazon.com/How-Mathematicians-Think-Contradiction-Mathematics/dp/0691145997
- "mathmagic land"
- I believe it was in fifth grade that I first saw this tribute to the beauty and power of math: https://en.wikipedia.org/wiki/Donald_in_Mathmagic_Land.
- multiplicative building blocks
- It is interesting to compare these building blocks with the additive building blocks, the powers of 2. Sums of 1, 2, 4, 8, etc., in all their combinations, suffice to generate all the nonnegative integers. (Zero, of course, is the combination that takes none of these powers of 2.)
- 1 is neither prime nor composite
- See http://numberphile.com/videos/1notprime.html (5:22) if you need convincing that 1 is indeed the loneliest number.
- 2 is the only even prime
- Which makes it the oddest prime of all, according to an old math joke. ☺
- can be perused and pursued
- From the book Prime Numbers, The Most Mysterious Figures in Math by David Wells: http://www.amazon.com/Prime-Numbers-Most-Mysterious-Figures/dp/1620458241.